Lighting and shadow casting algorithms can be very roughly divided into two categories; Direct Illumination and Global Illumination. Many people will be familiar with the former category, and the problems associated with it. This article will briefly discuss the two approaches, then give an in-depth study of one Global Illumination method, Radiosity.
There are all sorts of techniques under this heading: Shadow Volumes, Z-Buffer methods, Ray Tracing . . . But as a general rule, they all suffer from similar problems, and all require some kind of fudge in order to overcome them.
|
 |
 |
 |
It it quite common for people to claim that ray tracers and other renderers produce 'photo-realistic' results. But imagine someone were to show you a typical ray traced image, and claim it was a photo. You would claim in return that they were blind or lying.
It should also be noted that, in the real world, it is still possible to see objects that are not directly lit; shadows are never completely black. Direct Illumination renderers try to handle such situations by adding an Ambient Light term. Thus all objects receive a minimum amount of uni-directional light.
|
Lighting a simple scene with Direct LightingI modeled this simple scene in 3D Studio. I wanted the room to look as if it was lit by the sun shining in through the window.
So, I set up a spotlight to shine in. When I rendered it, the entire room was pitch black, except for a couple of patches on
the floor that the light reached. |
 |
Lighting a simple scene with Global LightingI modeled the same scene in my own radiosity renderer. To provide the source of light, I rendered an image of the sky with Terragen, and placed it outside the window. No other source of light was used.
With no further effort on my part, the room looks realistically lit.
|
 |
I would now like to ask an expert on shadows, who will explain to you everything they know about the subject. My expert is a tiny patch of paint on the wall in front of me.
hugo: "Why is it that you are in shadow, when a very similar patch of paint near you is in light?"
paint: "What do you mean?"
hugo: "How is it you know when to be in shadow, and when not to be? What do you know about shadow casting algorithms? You're just some paint."
paint: "Listen mate. I don't know what you're talking about. My job is a simple one: any light that hits me, I scatter back."
hugo: "Any light?"
paint: "Yes, any light at all. I don't have a preference."
So there you have it. The basic premise of Radiosity. Any light that hits a surface is reflected back into the scene. That's any light. Not just light that's come directly from light sources. Any light. That's how paint in the real world thinks, and that's how the radiosity renderer will work.
In my next article, I will be explaining how you can make your own talking paint.
So, the basic principal behind the radiosity renderer is to remove the distinction between objects and light sources. Now, you can
consider everything to be a potential light source.
Anything that is visible is either emitting or reflecting light, i.e. it is a source of light. A Light Source. Everything you can
see around you is a light source. And so, when we are considering how much light is reaching any part of a scene, we must take care
to add up light from all possible light sources.
Now that you have the important things in mind. I will take you through the process of performing Radiosity on a scene.
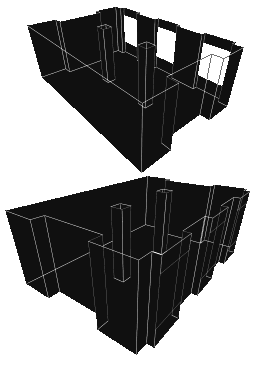 |
A Simple SceneWe begin with a simple scene: a room with three windows. There are a couple of pillars and some alcoves, to provide interesting shadows.It will be lit by the scenery outside the windows, which I will assume is completely dark, except for a small, bright sun. |
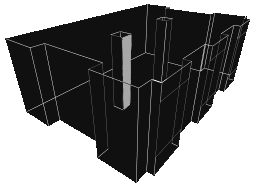 |
Now, lets choose one of the surfaces in the room, and consider the lighting on it. |
 |
As with many difficult problems in computer graphics, we'll divide it up into little patches (of paint), and try to see the world
from their point of view. From now on I'll refer to these patches of paint simply as patches.
|
 |
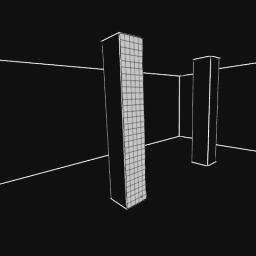
Take one of those patches. And imagine you are that patch. What does the world look like from that perspective? |
 |
View from a patchPlacing my eye very carefully on the patch, and looking outwards, I can see what it sees. The room is very dark, because no light has entered yet. But I have drawn in the edges for your benefit.By adding together all the light it sees, we can calculate the total amount of light from the scene reaching the patch. I'll refer to this as the total incident light from now on. This patch can only see the room and the darkness outside. Adding up the incident light, we would see that no light is arriving here. This patch is darkly lit. |
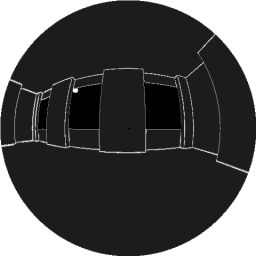 |
View from a lower patchPick a patch a little further down the pillar. This patch can see the bright sun outside the window. This time, adding up the incident light will show that a lot of light is arriving here (although the sun appears small, it is very bright). This patch is brightly lit. |
 |
Lighting on the PillarHaving repeated this process for all the patches, and added up the incident light each time, we can look back at the pillar and see what the lighting is like.The patches nearer the top of the pillar, which could not see the sun, are in shadow, and those that can are brightly lit. Those that could see the sun partly obscured by the edge of the window are only dimly lit. And so Radiosity proceeds in much the same fashion. As you have seen, shadows naturally appear in parts of the scene that cannot see a source of light. |
 |
Entire Room Lit: 1st PassRepeating the process for every patch in the room, gives us this scene. Everything is completely dark, except for surfaces that have received light from the sun.So, this doesn't look like a very well lit scene. Ignore the fact that the lighting looks blocky; we can fix that by using many more patches. What's important to notice is that the room is completely dark, except for those areas that can see the sun. At the moment it's no improvement over any other renderer. Well, it doesn't end here. Now that some parts of the room are brightly lit, they have become sources of light themselves, and could well cast light onto other parts of the scene. |
 |
View from the patch after 1st PassPatches that could not see the sun, and so received no light, can now see the light shining on other surfaces. So in the next pass, this patch will come out slightly lighter than the completely black it is now. |
 |
Entire Room Lit: 2nd PassThis time, when you calculate the incident light on each patch in the scene, many patches that were black before are now lit. The room is beginning to take on a more realistic appearance.What's happened is that sun light has reflected once from the floor and walls, onto other surfaces. |
 |
Entire Room Lit: 3rd PassThe third pass produces the effect of light having reflected twice in the scene. Everything looks pretty much the same, but is slightly brighter.The next pass only looks a little brighter than the last, and even the 16 th is not a lot different. There's not much point in doing any more passes after that. The radiosity process slowly converges on a solution. Each pass is a little less different than the last, until eventually it becomes stable. Depending on the complexity of the scene, and the lightness of the surfaces, it may take a few, or a few thousand passes. It's really up to you when to stop it, and call it done. |
 |
 |
| 4th Pass | 16th Pass |
Emmision
Though I have said that we'll consider lightsources and objects to be basically
the same, there must obviously be some source of light in the scene. In the
real world, some objects do emit light, and some don't, and all objects absorb
light to some extent. We must somehow distinguish between parts of the scene
that emit light, and parts that don't. We shall handle this in radiosity by
saying that all patches emit light, but for most patches, their light emmision
is zero. This property of a patch, I'll call emmision.
Reflectance
When light hits a surface, some light is absorbed and becomes heat, (we can
ignore this) and the rest is reflected. I'll call the proportion of light
reflected by a patch reflectance.
Incident and Excident Light
During each pass, it will be necessary to remember two other things, how
much light is arriving at each patch, and how much light is leaving each patch.
I'll call these two, incident_light and excident_light. The
excident light is the visible property of a patch. When we look at a patch,
it is the excident light that we're seeing.
incident_light = sum of all light that a patch can see
excident_light = (incident_light*reflectance) + emmision
Patch structure
Now that we know all the necessary properties of a patch, it's time to
define a patch. Later, I'll explain the details of the four variables.
structure PATCH
emmision
reflectance
incident
excident
end structure
Now that I've explained the basics of the algorithm, I'll tell it again in pseudocode form, to make it concrete. Clearly this is still quite high level, but I'll explain in more detail later.
|
Explanation of Code
initialise patches:
Passes Loop:
each patch collects light from the scene
calculate excident light from each patch: This process must be repeated many times to get a good effect. If the renderer needs another pass, then we jump back to Passes_Loop. |
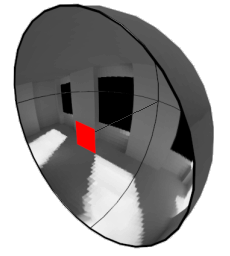 |
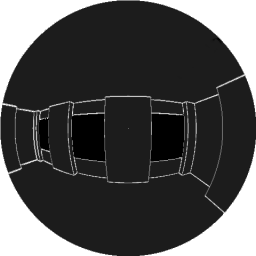
The Hemisphere Imagine a fish eye view wrapped onto a hemisphere. Place the hemisphere over a patch (left: red square), and from that patch's point of view, the scene wrapped on the inside of the hemisphere looks just like the scene from it's point of view. There's no difference. Placing a camera in the middle of the hemisphere, you can see that the view looks just like any other rendering of the scene (right). If you could find a way to render a fisheye view easily, then you could just sum up the brightness of every pixel to calculate the total incident light on the patch. However, it's not easy to render a fisheye view, and so some other way must be found to calculate the incident light. |
 Rendering from the centre of the hemisphere |
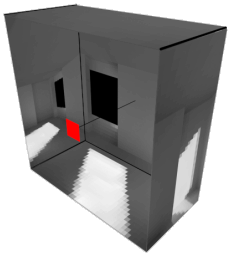 |
The Hemicube Surprisingly (or unsurprisingly, depending on how mathematical you are) a hemicube looks exactly the same as a hemisphere from the patch's point of view. |
 Rendering from the centre of the hemicube |

So, you can easily produce each of these images by placing a camera on a patch, and render it pointing forwards, up, down, left and right. The four side images are, of course, cut in half, and so, only half a rendering is required there.

|
This is view of 3 spheres, rendered with a 90° field of view. All three spheres are the same distance from the camera, but because of the properties of perspective transformation, objects at the edge of the image appear spretched and larger than ones in the middle. If this was the middle image of a hemicube, and the three spheres were light sources, then those near the edge would cast more light onto the patch than they should. This would be inaccurate, and so we must compensate for this. If you were to use a hemicube to calculate the total incident light falling on a patch, and just added together the values of all the pixel rendered in the hemicube, you would be giving an unfair weight to objects lying at the corners of the hemicube. They would appear to cast more light onto the patch. To compensate for this, it is necessary to 'dim' the pixels at the edges and corners, so that all objects contribute equally to the incident light, no matter where they may lie in the hemicube. Rather than give a full explanation, I'm just going to tell you how this is done. |

|
Pixels on a surface of the hemicube are multiplied by the cosine of the angle between the direction the camera is facing in, and the line from the camera to the pixel. On the left is an image of the map used to compensate for the distortion. (shown half size relative to the image above) |

|
Any budding graphics programmer knows Lambert's cosine law: The apparent brightness of a surface is proportional to the cosine of
the angle between the surface normal, and the direction of the light. Therefore, we should be sure to apply the same law here. This
is simply done by multiplying pixels on the hemicube by the relevant amount. On the left is an image of the map used to apply Lambert's law to the hemicube. White represents the value 1.0, and black represents the value 0.0. (shown half size relative to the image above) |

|
Now pay attention, this is important: Multiplying the two maps together gives this. This map is essential for producing an accurate radiosity solution. It is used to adjust for the perspective distortion, mentioned above, that causes objects near the corners of the hemicubes to shine too much light onto a patch. It also gives you Lambert's Cosine Law. Having created this map, you should have the value 1.0 right at the centre, and the value 0.0 at the far corners. Before it can be used, the map must be normalised. The sum of all pixels in the map should be 1.0.
|

First, it renders the 5 faces of the hemicube using the procedure RenderView(point, vector, part). This procedure takes as it's arguments a point, telling it where the camera should be for the rendering, a vector, telling it what direction the camera should be pointing in, and another argument telling it which part of the final image should be rendered. These 5 images are stored in hemicube structure called H (left column of images below).
Once the hemicube H has been rendered, it is multiplied by the multiplier hemicube M (middle column of images below), and the result is stored in the hemicube R (right column of images below).
Then the total value of the light in R is added up and divided by the number of pixels in a hemicube. This should give the total amount of light arriving at the point in question.
|

|
structure light
float Red
float Green
float Blue
end structure
hemicube: used for storing the view of a scene from the point of view of some point in the scene. A Hemicube would consist of five images, as illustrated above, where each pixel was of type light. In the case of the Multiplier Hemicube, what is stored is not a value of light, but some multiplier value less than 1.0, as illustrated above.
structure hemicube
image front
image up
image down
image left
image right
end structure
camera: for example
structure camera
point lens
vector direction
end structure
Fortunately, this is something people have been doing since the dawn of time. Um, since the dawn of the raster display, and since then there has been much work put into rendering texture mapped scenes as fast as possible. I won't go into a whole lot of detail here, I'm really not the person best qualified to be talking about optimised rendering. My own renderer is so slow you have to use cussing words to describe it. The algorithm also lends itself well to optimisation with standard 3D graphics hardware, though you have do some fiddling and chopping to get it to render (3x32) bit textures.
The speed improvement I'm going to discuss in this article does not concern optimising the actual rendering of the hemicubes, but rather reducing the number of hemicubes that need to be rendered. You will, of course, have noticed that the light maps illustrated in the black and white renderings above were somewhat blocky, low resolution. Don't fear, their resolution can be increased as far as you want.

|
Take a look at the surface on the left, outlined in red. The lighting is basically very simple, there's a bright bit, and a less
bright bit, with a fairly sharp edge between the two. To reproduce the edge sharply, you would normally need a high resolution
light map and, therefore, have to render very many hemicubes. But it hardly seems worthwhile rendering so many hemicubes just to
fill in the bright or less-bright areas which are little more than solid colour. It would be more worthwhile to render a lot of
hemicubes near the sharp edge, and just a few in the other areas. Well, it is possible, and quite straightforward. The algorithm I will describe below will render a few hemicubes scattered across the surface, then render more near the edges, and use linear interpolation to fill in the rest of the light map. |
|
The Algorithm: On the far left you can see the light map in the process of being generated. Next to it, you can see which
pixels were produced using a hemicube (red) and which were linearly interpolated (green).
|
||
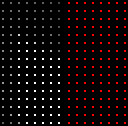 |
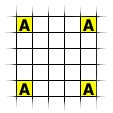
1:
Use a hemicube to calculate every 4th pixel.
I'll show these pixels on the right as |
 |
 |
2:
Pass Type 1: Examine the pixels |
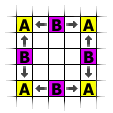 |
 |
3:
Pass Type 2: Examine the pixels |
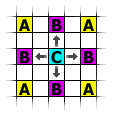 |
 |
4: Pass Type 1: Same as step 2, but with half the spacing. |  |
 |
5: Pass Type 2: Same as step 3, but with half the spacing. |  |
You should be able to see, from the maps on the left, that most of the light map was produced using linear interpolation. In fact, from a total of 1769 pixels, only 563 were calculated by hemicube, and 1206 by linear interpolation. Now, since rendering a hemicube takes a very long time indeed, compared to the negligable time required to do a linear interpolation, it represents a speed improvement of about 60% !
Now, this method is not perfect, and it can occasionally miss very small details in a light map, but it's pretty good in most situations. There's a simple way to help it catch small details, but I'll leave that up to your own imagination.
#### CODE EDITING IN PROGRESS - BIT MESSY STILL ####
float ratio2(float a, float b)
{
if ((a==0) && (b==0)) return 1.0;
if ((a==0) || (b==0)) return 0.0;
if (a>b) return b/a;
else return a/b;
}
float ratio4(float a, float b, float c, float d)
{
float q1 = ratio2(a,b);
float q2 = ratio2(c,d);
if (q1<q2) return q1;
else return q2;
}
procedure CalcLightMap()
vector normal = LightMap.Surface_Normal
float Xres = LightMap.X_resolution
float Yres = LightMap.Y_resolution
point3D SamplePoint
light I1, I2, I3, I4
Accuracy = Some value greater than 0.0, and less than 1.0.
Higher values give a better quality Light Map (and a slower render).
0.5 is ok for the first passes of the renderer.
0.98 is good for the final pass.
Spacing = 4 Higher values of Spacing give a slightly faster render, but
will be more likely to miss fine details. I find that 4 is
a pretty reasonable compromise.
// 1: Initially, calculate an even grid of pixels across the Light Map.
// For each pixel calculate the 3D coordinates of the centre of the patch that
// corresponds to this pixel. Render a hemicube at that point, and add up
// the incident light. Write that value into the Light Map.
// The spacing in this grid is fixed. The code only comes here once per Light
// Map, per render pass.
for (y=0; y<Yres; y+=Spacing)
for (x=0; x<Xres; x+=Spacing)
{
SamplePoint = Calculate coordinates of centre of patch
incidentLight = Calc_Incident_Light(SamplePoint, normal)
LightMap[x, y] = incidentLight
}
// return here when another pass is required
Passes_Loop:
threshold = pow(Accuracy, Spacing)
// 2: Part 1.
HalfSpacing = Spacing/2;
for (y=HalfSpacing; y<=Yres+HalfSpacing; y+=Spacing)
{
for (x=HalfSpacing; x<=Xres+HalfSpacing; x+=Spacing)
{
// Calculate the inbetween pixels, whose neighbours are above and below this pixel
if (x<Xres) // Don't go off the edge of the Light Map now
{
x1 = x
y1 = y-HalfSpacing
// Read the 2 (left and right) neighbours from the Light Map
I1 = LightMap[x1+HalfSpacing, y1]
I2 = LightMap[x1-HalfSpacing, y1]
// If the neighbours are very similar, then just interpolate.
if ( (ratio2(I1.R,I2.R) > threshold) &&
(ratio2(I1.G,I2.G) > threshold) &&
(ratio2(I1.B,I2.B) > threshold) )
{
incidentLight.R = (I1.R+I2.R) * 0.5
incidentLight.G = (I1.G+I2.G) * 0.5
incidentLight.B = (I1.B+I2.B) * 0.5
LightMap[x1, y1] = incidentLight
}
// Otherwise go to the effort of rendering a hemicube, and adding it all up.
else
{
SamplePoint = Calculate coordinates of centre of patch
incidentLight = Calc_Incident_Light(SamplePoint, normal)
LightMap[x1, y1] = incidentLight
}
}
// Calculate the inbetween pixels, whose neighbours are left and right of this pixel
if (y<Yres) // Don't go off the edge of the Light Map now
{
x1 = x-HalfSpacing
y1 = y
// Read the 2 (up and down) neighbours from the Light Map
I1 = LightMap[x1,y1-HalfSpacing];
I2 = LightMap[x1,y1+HalfSpacing];
// If the neighbours are very similar, then just interpolate.
if ( (ratio2(I1.R,I2.R) > threshold) &&
(ratio2(I1.G,I2.G) > threshold) &&
(ratio2(I1.B,I2.B) > threshold) )
{
incidentLight.R = (I1.R+I2.R) * 0.5
incidentLight.G = (I1.G+I2.G) * 0.5
incidentLight.B = (I1.B+I2.B) * 0.5
LightMap[x1,y1] = incidentLight
}
// Otherwise go to the effort of rendering a hemicube, and adding it all up.
else
{
SamplePoint = Calculate coordinates of centre of patch
incidentLight = Calc_Incident_Light(SamplePoint, normal)
LightMap[x1, y1] = incidentLight
}
}//end if
}//end x loop
}//end y loop
// 3: Part 2
// Calculate the pixels, whose neighbours are on all 4 sides of this pixel
for (y=HalfSpacing; y<=(Yres-HalfSpacing); y+=Spacing)
{
for (x=HalfSpacing; x<=(Xres-HalfSpacing); x+=Spacing)
{
I1 = LightMap[x, y-HalfSpacing]
I2 = LightMap[x, y+HalfSpacing]
I3 = LightMap[x-HalfSpacing, y]
I4 = LightMap[x+HalfSpacing, y]
if ( (ratio4(I1.R,I2.R,I3.R,I4.R) > threshold) &&
(ratio4(I1.G,I2.G,I3.G,I4.G) > threshold) &&
(ratio4(I1.B,I2.B,I3.B,I4.B) > threshold) )
{
incidentLight.R = (I1.R + I2.R + I3.R + I4.R) * 0.25
incidentLight.G = (I1.G + I2.G + I3.G + I4.G) * 0.25
incidentLight.B = (I1.B + I2.B + I3.B + I4.B) * 0.25
LightMap[x,y] = incidentLight
}
else
{
SamplePoint = Calculate coordinates of centre of patch
incidentLight = Calc_Incident_Light(SamplePoint, normal)
LightMap[x, y] = incidentLight;
}
}
}
Spacing = Spacing / 2
Stop if Spacing = 1, otherwise go to Passes_Loop
|
|
It is generally considered that Radiosity does not deal well with point light sources. This is true to some extent, but it is not
impossible to have reasonable point light sources in your scene. I tried adding bright, point sized objects to my scenes, that were rendered as wu-pixels. When a hemicube was rendered, they would appear in the hemicube as bright points, thus shining light onto patches. They almost worked, but were subject to some unacceptable artifacts. The scene on the right was lit by three point spot lights; two on the pillars at the back, and one near the top-left, pointing towards the camera. The scene appears fine from this angle, but nasty artifacts are apparent if I turn the camera around.
|

|
|
You can see, on the
bottom image, three dark lines along the wall and floor. These were caused by the the light source seeming to get lost at the very edges
of the hemicubes. Perhaps this wouldn't have been so bad if I'd got my maths absolutely perfect and the edges of the hemicubes matched perfectly, but I'm sure that there would still have been noticable artifacts. So, rather than rendering the point lights onto the hemicubes, you can use ray tracing to cast the light from point sources onto patches. |

|

How you go about this optimisation might not be quite what you expect, but it works well, letting the CPU and rendering hardware work together in parallel. The hardware handles the texture mapping and hidden surface removal (z-buffering), and the CPU handles the rest of the radiosity.
As far as I know, there is no rendering hardware that deals with floating point lighting values, or even lighting values above 255. So there is no point trying to get them to directly render scenes with such lighting. However, with a little subtlety, you can get them to do the texture mapping and hidden surface removal, while you put the lighting back in with a simple, fast loop.
If 3D hardware can write 32-bit pixels to the screen, then it can be made to write 32-bit values representing anything we want. 3D hardware can't write actual floating point RGBs to the screen, but it can write 32-bit pointers to the patches that should be rendered there. Once it's done that, you simply need to take each pixel, and use it's 32-bit value as an address to locate the patch that should have been rendered there.
| Here is one of the patch maps from the scene above. Each pixel has a floating point value for Red, Green and Blue. And so 3D hardware will not be able to deal with this directly. |

|

|
Now this is another map. It looks totally weird, but ignore how it looks for now. Each pixel in this
map is actually a 32-bit value, which is the address of the corresponding pixel on the left. The reason the colours appear is because the lowest three bytes in the address are interpreted as colours. |
|
Once you make a whole set of these pointer textures (one for each surface in your scene), you can
give them to the 3D hardware to render with them. The scene it comes out with will look something like this (right). The scene looks totally odd, but you can make out surfaces covered with patterns similar to the one above. The pixels should not be interpreted as colours, but as pointers. If your graphics card used 32-bit textures, then they will be in a form something like ARGB, with A, R G and B being 8-bit values. Ignore this structure and treat each pixel as a 32-bit value. Use them as memory pointers back to the patches that should be there, and recreate the scene properly with patches. Important: You must make sure that you render the scene purely texture mapped. That means: NO linear interpolation, NO anti-aliasing, NO motion blur, NO shading/lighting, NO Mip Mapping, NO Fog, NO Gamma Correction or anything else that isn't just a straight texture map. If you do not do this, the adresses produced will not point to the correct place, and your code will almost certainally crash. |

|
Your average monitor can at best produce only dim light, not a lot brighter than a surface indoors. Clearly you cannot display your image directly on a monitor. To do this would require a monitor that could produce light as bright as the sun, and a graphics card with 32 bits per channel. These things don't exist for technical, not to mention safety, issues. So what can you do?
Most people seem to be happy to look at photographs and accept them as faithful representations of reality. They are wrong. Photographs are no better than monitors for displaying real-life bright images. Photographs cannot give off light as bright as the sun, but people never question their realism. Now this is where confusion sets in.
Try this: Go out in a totally overcast day. Stand infront of something white. If you look at the clouds, you will see them as being grey, but look at the white object, and it appears to be white. So what? Well the white thing is lit by the grey clouds and so can't possibly be any brighter than them (in fact it will be darker), and yet we still perceive it to be white. If you don't believe me, take a photo showing the white thing and the sky in the background. You will see that the white thing looks darker than the clouds.
Don't trust your eyes: They are a hell of a lot smarter than you are.
So what can you do? Well, since people are so willing to accept photographs as representations of reality we can take the output of the renderer, which is a physical model of the light in a scene, and process this with a rough approximation of a camera film. I have already written an article on this: Exposure, so I will say no more about it here.
References
The Solid Map:
Methods for Generating a 2D Texture Map
for Solid Texturing: http://graphics.cs.uiuc.edu/~jch/papers/pst.pdf
This paper will be very useful if you are going to try to implement your own
radiosity renderer. How do you apply a texture map evenly, and without distortion across some
arbitary polygonal object? A radiosity renderer will need to do this.
Helios32: http://www.helios32.com/
Offers a platform-independent solution for developers looking for radiosity rendering capabilities.
Radiosity In English:
http://www.flipcode.com/tutorials/tut_rad.shtml
As the title suggests this is an article about Radiosity, written using English words. I didn't understand it.
Real Time Radiosity: http://www.gamedev.net/reference/programming/features/rtradiosity2/
That sounds a little more exciting. There doesn't seem to be a demo though.
An Empirical Comparison of Radiosity Algorithms: http://www.cs.cmu.edu/~radiosity/emprad-tr.html
A good technical article comparing matrix, progressive, and wavelet radiosity algorithms. Written by a couple of
the masters.
A Rapid Hierarchical Radiosity Algorithm: http://graphics.stanford.edu/papers/rad/
A paper that presents a rapid hierarchical radiosity algorithm for illuminating scenes containing large polygonal patches.
KODI's Radiosity Page : http://ls7-www.informatik.uni-dortmund.de/~kohnhors/radiosity.html
A whole lot of good radiosity links.
Graphic Links: http://web.tiscalinet.it/GiulianoCornacchiola/Eng/GraphicLinks6.htm
Even more good links.
Rover: Radiosity for Virtual Reality Systems: http://www.scs.leeds.ac.uk/cuddles/rover/
*Very Good* A thesis on Radiosity. Contains a large selection of good articles on radiosity, and
very many abstracts of papers on the subject.
Daylighting Design:
http://www.arce.ukans.edu/book/daylight/daylight.htm
A very indepth article about daylight.
|
|

|