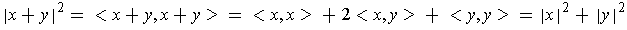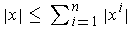 .
.
One has
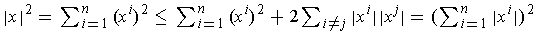 .
Taking the square root of both sides gives the result.
.
Taking the square root of both sides gives the result.
Equality holds precisely when one is a nonnegative multiple of the other. This is a consequence of the analogous assertion of the next problem.
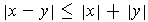 . When does equality hold?
. When does equality hold?
The first assertion is the triangle inequality. I claim that equality holds precisely when one vector is a non-positive multiple of the other.
If
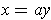 for some real
for some real
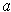 , then substituting shows that the inequality
, then substituting shows that the inequality
is equivalent to
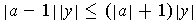 and clearly equality holds if
a is non-positive. Similarly, one has equality if
and clearly equality holds if
a is non-positive. Similarly, one has equality if
![]() for some real
for some real
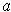 .
.
Conversely, if equality holds, then
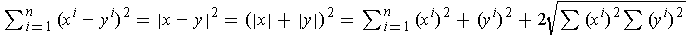 ,
and so
,
and so
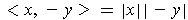 . By Theorem 1-1 (2), it follows that
. By Theorem 1-1 (2), it follows that
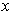 and
and
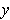 are linearly dependent. If
are linearly dependent. If
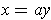 for some real
for some real
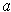 , then substituting
back into the equality shows that
, then substituting
back into the equality shows that
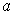 must be non-positive or
must be non-positive or
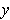 must be 0.
The case where
must be 0.
The case where
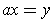 is treated similarly.
is treated similarly.
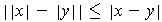 .
.
If
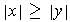 , then the inequality to be proved is just
, then the inequality to be proved is just
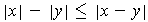 which is just the triangle inequality. On the other hand, if
which is just the triangle inequality. On the other hand, if
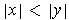 ,
then the result follows from the first case by swapping the roles of
,
then the result follows from the first case by swapping the roles of
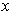 and
and
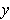 .
.
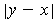 is called the distance between
is called the distance between
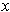 and
and
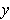 .
Prove and interpret geometrically the ``triangle inequality":
.
Prove and interpret geometrically the ``triangle inequality":
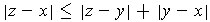 .
.
The inequality follows from Theorem 1-1(3):
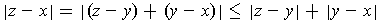
Geometrically, if
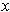 ,
,
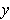 , and
, and
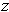 are the vertices of a triangle, then the
inequality says that the length of a side is no larger than the sum of the
lengths of the other two sides.
are the vertices of a triangle, then the
inequality says that the length of a side is no larger than the sum of the
lengths of the other two sides.
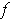 and
and
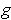 be functions integrable on
be functions integrable on
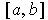 .
.
-
Prove that
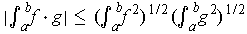 .
.
Theorem 1-1(2) implies the inequality of Riemann sums:
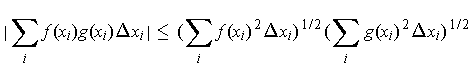
Taking the limit as the mesh approaches 0, one gets the desired inequality.
-
If equality holds, must
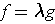 for some
for some
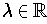 ?
What if
?
What if
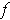 and
and
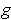 are continuous?
are continuous?
No, you could, for example, vary
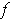 at discrete points without changing the
values of the integrals. If
at discrete points without changing the
values of the integrals. If
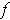 and
and
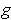 are continuous, then the assertion
is true.
are continuous, then the assertion
is true.
In fact, suppose that for each
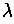 , there is an
, there is an
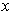 with
with
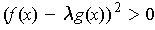 .
Then the inequality holds true in an open neighborhood of
.
Then the inequality holds true in an open neighborhood of
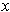 since
since
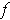 and
and
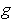 are
continuous. So
are
continuous. So
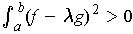 since the integrand is always
non-negative and is positive on some subinterval of
since the integrand is always
non-negative and is positive on some subinterval of
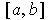 . Expanding out
gives
. Expanding out
gives
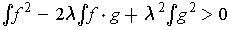 for all
for all
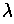 . Since the quadratic has no solutions, it must be that its
discriminant is negative.
. Since the quadratic has no solutions, it must be that its
discriminant is negative.
-
Show that Theorem 1-1 (2) is a special case of (a).
Let
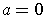 ,
,
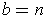 ,
,
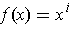 and
and
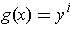 for all
for all
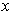 in
in
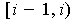 for
for
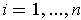 . Then part (a) gives the inequality of Theorem 1-1 (2).
Note, however, that the equality condition does not follow from (a).
. Then part (a) gives the inequality of Theorem 1-1 (2).
Note, however, that the equality condition does not follow from (a).
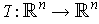 is called
norm preserving if
is called
norm preserving if
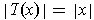 , and inner product preserving
if
, and inner product preserving
if
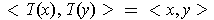 .
.
-
Show that
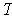 is norm preserving if and only if
is norm preserving if and only if
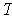 is inner product
preserving.
is inner product
preserving.
If
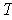 is inner product preserving, then one has by Theorem 1-1 (4):
is inner product preserving, then one has by Theorem 1-1 (4):
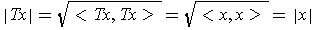
Similarly, if
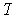 is norm preserving, then the polarization identity together
with the linearity of T give:
is norm preserving, then the polarization identity together
with the linearity of T give:
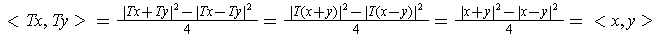 .
.
-
Show that such a linear transformation
 is 1-1, and that
is 1-1, and that
 is of the same sort.
is of the same sort.
Let
 be norm preserving. Then
be norm preserving. Then
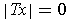 implies
implies
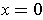 , i.e. the kernel
of
, i.e. the kernel
of
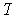 is trivial. So T is 1-1. Since
is trivial. So T is 1-1. Since
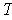 is a 1-1 linear map of a finite
dimensional vector space into itself, it follows that
is a 1-1 linear map of a finite
dimensional vector space into itself, it follows that
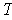 is also onto. In
particular,
is also onto. In
particular,
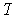 has an inverse. Further, given
has an inverse. Further, given
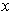 , there is a
, there is a
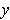 with
with
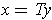 , and so
, and so
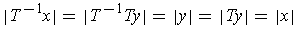 , since
, since
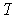 is
norm preserving. Thus
is
norm preserving. Thus
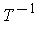 is norm preserving, and hence also inner
product preserving.
is norm preserving, and hence also inner
product preserving.
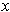 and
and
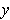 in
in
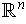 are both non-zero, then the angle
between
are both non-zero, then the angle
between
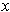 and
and
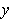 , denoted
, denoted
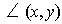 , is defined to be
, is defined to be
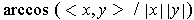 which makes sense by Theorem 1-1 (2). The linear transformation
which makes sense by Theorem 1-1 (2). The linear transformation
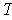 is
angle preserving if
is
angle preserving if
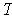 is 1-1 and for
is 1-1 and for
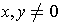 , one has
, one has
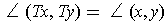 .
.
- Prove that if
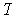 is norm preserving, then
is norm preserving, then
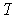 is angle preserving.
is angle preserving.
Assume
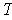 is norm preserving. By Problem 1-7,
is norm preserving. By Problem 1-7,
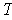 is inner product preserving.
So
is inner product preserving.
So
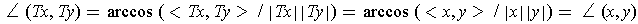 .
.
-
If there is a basis
 of
of
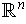 and numbers
and numbers
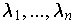 such that
such that
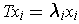 , prove that
, prove that
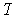 is angle preserving if and only if all
is angle preserving if and only if all
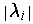 are equal.
are equal.
The assertion is false. For example, if
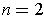 ,
,
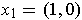 ,
,
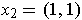 ,
,
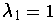 , and
, and
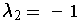 , then
, then
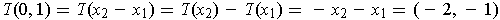 . Now,
. Now,
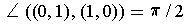 ,
but
,
but
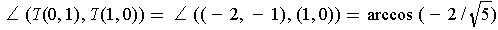 showing
that T is not angle preserving.
showing
that T is not angle preserving.
To correct the situation, add the condition that the
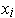 be pairwise
orthogonal, i.e.
be pairwise
orthogonal, i.e.
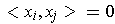 for all
for all
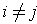 . Using bilinearity,
this means that:
. Using bilinearity,
this means that:
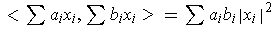 because
all the cross terms are zero.
because
all the cross terms are zero.
Suppose all the
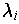 are equal in absolute value. Then one has
are equal in absolute value. Then one has
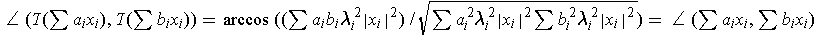 because all the
because all the
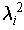 are equal and
cancel out. So, this condition suffices to make
are equal and
cancel out. So, this condition suffices to make
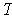 be angle preserving.
be angle preserving.
Now suppose that
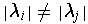 for some
for some
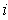 and
and
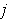 and that
and that
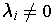 . Then
. Then
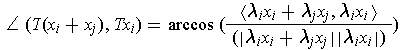
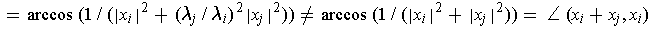
since
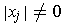 .
So, this condition suffices to make
.
So, this condition suffices to make
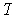 not be angle preserving.
not be angle preserving.
-
What are all angle preserving
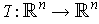 ?
?
The angle preserving
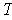 are precisely those which can be expressed in the
form
are precisely those which can be expressed in the
form
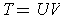 where U is angle preserving of the kind in part (b), V is
norm preserving, and the operation is functional composition.
where U is angle preserving of the kind in part (b), V is
norm preserving, and the operation is functional composition.
Clearly, any
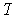 of this form is angle preserving as the composition of two
angle preserving linear transformations is angle preserving. For the
converse, suppose that
of this form is angle preserving as the composition of two
angle preserving linear transformations is angle preserving. For the
converse, suppose that
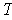 is angle preserving. Let
is angle preserving. Let
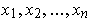 be
an orthogonal basis of
be
an orthogonal basis of
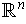 . Define
. Define
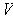 to be the linear
transformation such that
to be the linear
transformation such that
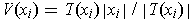 for each
for each
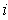 .
Since the
.
Since the
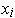 are pairwise orthogonal and
are pairwise orthogonal and
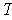 is angle preserving, the
is angle preserving, the
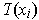 are also pairwise orthogonal. In particular,
are also pairwise orthogonal. In particular,
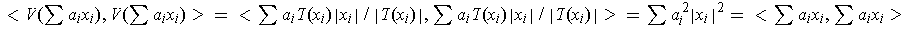 because the cross terms
all cancel out. This proves that
because the cross terms
all cancel out. This proves that
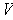 is norm preserving. Now define
is norm preserving. Now define
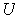 to
be the linear transformation
to
be the linear transformation
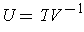 . Then clearly
. Then clearly
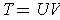 and
and
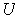 is angle preserving because it is the composition of two angle preserving
maps. Further,
is angle preserving because it is the composition of two angle preserving
maps. Further,
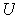 maps each
maps each
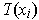 to a scalar multiple of itself; so
to a scalar multiple of itself; so
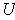 is a map of the type in part (b). This completes the characterization.
is a map of the type in part (b). This completes the characterization.
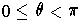 , let
, let
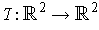 have the matrix
have the matrix
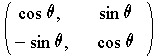 . Show that
. Show that
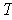 is angle
preserving and that if
is angle
preserving and that if
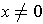 , then
, then
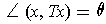 .
.
The transformation
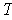 is 1-1 by Cramer's Rule because the determinant of
its matrix is 1. Further,
is 1-1 by Cramer's Rule because the determinant of
its matrix is 1. Further,
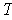 is norm preserving since
is norm preserving since
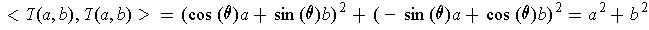
by the Pythagorean Theorem. By Problem 8(a), it follows that
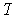 is angle
preserving.
is angle
preserving.
If
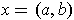 , then one has
, then one has
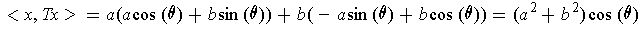 .
Further, since
.
Further, since
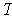 is norm preserving,
is norm preserving,
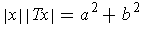 . By the definition
of angle, it follows that
. By the definition
of angle, it follows that
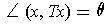 .
.
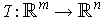 is a linear transformation, show
that there is a number
is a linear transformation, show
that there is a number
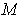 such that
such that
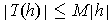 for
for
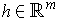 .
.
Let
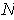 be the maximum of the absolute values of the entries in the matrix of
be the maximum of the absolute values of the entries in the matrix of
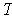 and
and
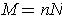 . One has
. One has
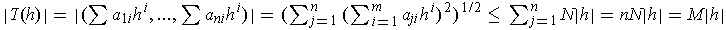 . (Correction: Bound should be square root of n times mN.)
. (Correction: Bound should be square root of n times mN.)
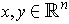 and
and
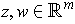 , show that
, show that
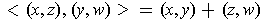 and
and
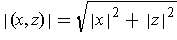 .
Note that
.
Note that
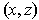 and
and
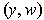 denote points in
denote points in
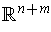 .
This is a perfectly straightforward computation in terms of the coordinates
of
.
This is a perfectly straightforward computation in terms of the coordinates
of
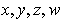 using only the definitions of inner product and norm.
using only the definitions of inner product and norm.
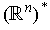 denote the dual space of the vector space
denote the dual space of the vector space
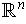 .
If
.
If
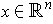 , define
, define
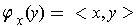 . Define
. Define
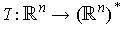 by
by
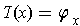 . Show that
. Show that
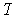 is a 1-1
linear transformation and conclude that every
is a 1-1
linear transformation and conclude that every
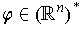 is
is
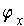 for a unique
for a unique
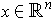 .
.
One needs to verify the trivial results that (a)
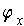 is a linear
tranformation and (b)
is a linear
tranformation and (b)
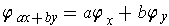 . These
follow from bilinearity; the proofs
are omitted. Together these imply that
. These
follow from bilinearity; the proofs
are omitted. Together these imply that
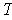 is a linear transformation.
is a linear transformation.
Since
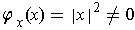 for
for
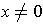 ,
,
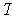 has no non-zero vectors
in its kernel and so is 1-1. Since the dual space has dimension n, it follows
that
has no non-zero vectors
in its kernel and so is 1-1. Since the dual space has dimension n, it follows
that
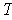 is also onto. This proves the last assertion.
is also onto. This proves the last assertion.
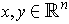 , then
, then
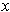 and
and
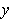 are called
perpendicular (or orthogonal) if
are called
perpendicular (or orthogonal) if
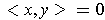 . If
. If
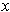 and
and
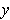 are perpendicular, prove that
are perpendicular, prove that
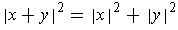 .
.
By bilinearity of the inner product, one has for perpendicular
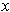 and
and
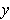 :
: