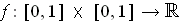 be defined by
be defined by
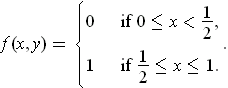
Show that
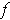 is integrable and that
is integrable and that
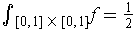 .
.
Apply Theorem 3-3 to the partition
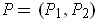 where
where
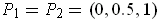 . For this partition,
. For this partition,
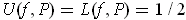 .
.
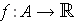 be integrable and let
be integrable and let
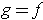 except at finitely many points. Show that
except at finitely many points. Show that
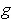 is integrable and
is integrable and
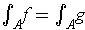 .
.
For any
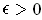 , there is a partition of
, there is a partition of
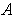 in which every subrectangle
has volume less than
in which every subrectangle
has volume less than
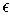 . In fact, if you partition
. In fact, if you partition
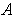 by dividing
each side into
by dividing
each side into
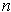 equal sized subintervals and
equal sized subintervals and
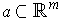 , then
the volume of each subrectangle is precisely
, then
the volume of each subrectangle is precisely
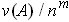 which is less than
which is less than
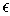 as soon as
as soon as
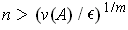 . Furthermore, if
. Furthermore, if
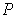 is
any partition, then any common refinement of this partition and
is
any partition, then any common refinement of this partition and
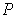 has the
same property.
has the
same property.
If
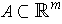 and
and
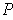 is a partition of
is a partition of
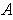 , then any point
, then any point
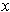 is
an element of at most
is
an element of at most
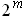 of the subrectangles of
of the subrectangles of
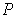 . The intuitive iddea
of the proof is that the worst case is when the point is in a `corner'; the
real proof is of course an induction on m.
. The intuitive iddea
of the proof is that the worst case is when the point is in a `corner'; the
real proof is of course an induction on m.
Let
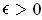 and
and
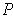 be a partition as in Theorem 3-3 applied to
be a partition as in Theorem 3-3 applied to
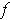 and
and
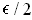 . Let
. Let
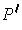 be a refinement of
be a refinement of
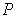 such that every subrectangle
of
such that every subrectangle
of
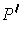 has volume less than
has volume less than
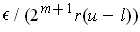 where
where
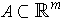 ,
,
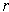 is the number of points where
is the number of points where
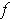 and
and
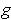 have values which differ, and
have values which differ, and
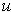 (resp.
(resp.
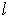 ) are upper (resp. lower) bounds for the values
) are upper (resp. lower) bounds for the values
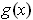 for all
for all
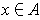 . Then the hypotheses of Theorem 3-3 are
satisfied by
. Then the hypotheses of Theorem 3-3 are
satisfied by
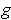 and
and
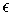 , and so
, and so
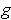 is integrable.
is integrable.
In fact,
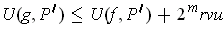 and
and
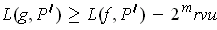 where
where
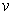 is any upper bound for the volume of the subrectangles of
is any upper bound for the volume of the subrectangles of
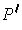 ,
because the terms of the sum can differ only on those subrectangles which
contain at least one of the
,
because the terms of the sum can differ only on those subrectangles which
contain at least one of the
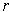 points where
points where
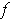 and
and
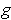 differ. Taking
differences gives
differ. Taking
differences gives
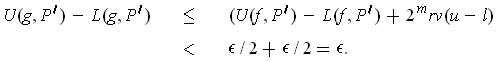
 be integrable.
be integrable.
- For any partition
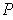 of
of
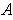 and any subrectangle
and any subrectangle
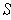 of
of
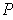 ,
show that
,
show that
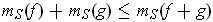 and
and
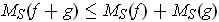 and therefore
and therefore
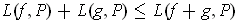 and
and
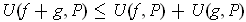 .
.
For each
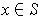 , one has
, one has
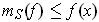 and
and
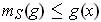 since
greatest lower bounds are lower bounds. Adding these inequalities shows
that
since
greatest lower bounds are lower bounds. Adding these inequalities shows
that
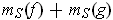 is a lower bound for
is a lower bound for
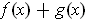 , and so it is at most
equal to the greatest lower bound of these values. A similar argument shows
the result for
, and so it is at most
equal to the greatest lower bound of these values. A similar argument shows
the result for
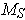 . Since
. Since
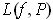 ,
,
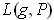 , and
, and
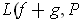 are just
positively weighted sums of the
are just
positively weighted sums of the
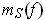 ,
,
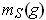 , and
, and
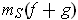 the result for
the result for
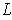 can be obtained by summing (with weights) the inequalities for the
can be obtained by summing (with weights) the inequalities for the
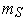 .
A similar argument shows the result for
.
A similar argument shows the result for
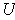 .
.
- Show that
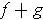 is integrable and
is integrable and
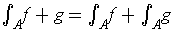 .
.
Let
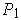 (resp.
(resp.
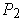 ) be a partition as in Theorem 3-3 applied to
) be a partition as in Theorem 3-3 applied to
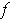 (resp.
(resp.
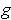 ) and
) and
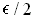 . Let
. Let
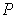 be a common refinement of
be a common refinement of
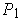 and
and
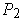 .
Then by part (a) and Lemma 3-1,
.
Then by part (a) and Lemma 3-1,
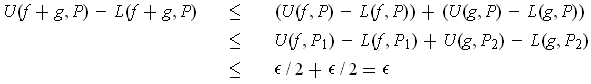
. By Theorem 3-3,
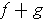 is integrable.
is integrable.
Further
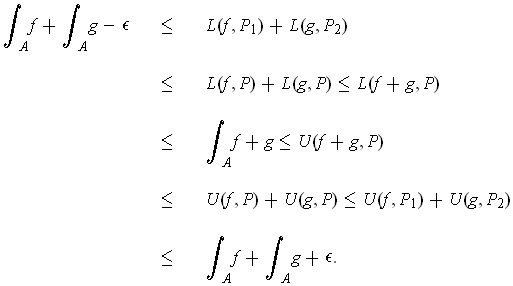
By the squeeze principle, one concludes that
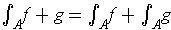 .
.
- For any constant
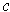 , show that
, show that
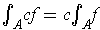 .
.
We will show the result in the case where
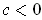 ; the other case being proved
in a similar manner. Let
; the other case being proved
in a similar manner. Let
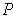 be a partition as in Theorem 3-3 applied to
be a partition as in Theorem 3-3 applied to
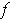 and
and
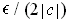 . Since
. Since
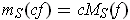 and
and
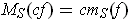 for each subrectangle
for each subrectangle
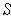 of
of
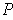 , we have
, we have
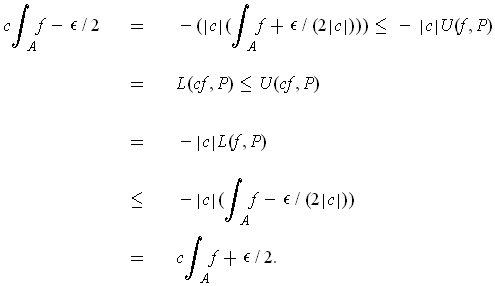
By Theorem 3-3, applied to
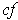 and
and
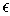 , the function
, the function
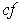 is integrable;
by the squeeze principle, its integral is
is integrable;
by the squeeze principle, its integral is
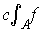 .
.
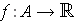 and
and
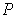 be a partition of
be a partition of
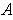 . Show
that
. Show
that
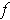 is integrable if and only if for each subrectangle
is integrable if and only if for each subrectangle
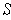 the function
the function
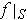 ,
which consists of
,
which consists of
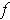 restricted to
restricted to
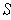 , is integrble, and that in this case
, is integrble, and that in this case
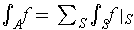 .
.
Suppose that
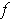 is integrable and
is integrable and
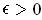 . Let
. Let
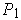 be a
partition of
be a
partition of
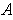 as in Theorem 3-3 applied to
as in Theorem 3-3 applied to
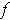 and
and
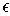 .
Let
.
Let
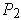 be a common refinement of
be a common refinement of
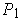 and
and
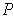 . Then there is a partition
. Then there is a partition
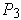 of
of
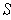 whose subrectangles are precisely the subrectangles of
whose subrectangles are precisely the subrectangles of
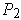 which are contained in
which are contained in
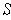 . Then
. Then
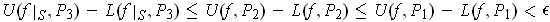 . By Theorem 3-3, it follows
that
. By Theorem 3-3, it follows
that
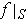 is integrable.
is integrable.
Suppose that all the
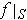 are integrable where
are integrable where
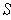 is any subrectangle of
is any subrectangle of
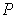 . Let
. Let
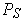 be a partition as in Theorem 3-3 applied to
be a partition as in Theorem 3-3 applied to
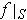 and
and
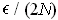 where
where
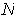 is the number of rectangles in
is the number of rectangles in
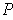 . Let
. Let
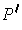 be the
partition of A obtained by taking the union of all the subsequences
defining the partitions of the
be the
partition of A obtained by taking the union of all the subsequences
defining the partitions of the
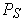 (for each dimension). Then there are
refinements
(for each dimension). Then there are
refinements
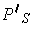 of the
of the
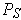 whose rectangles are the set of all subrectangles
of
whose rectangles are the set of all subrectangles
of
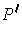 which are contained in
which are contained in
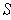 . One has
. One has
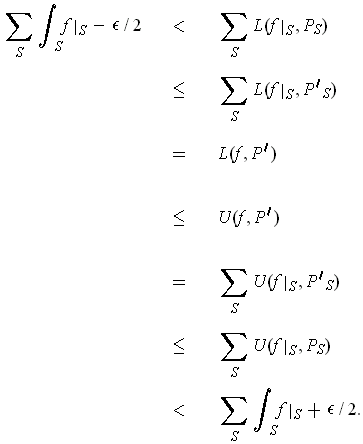
By Theorem 3-3, the
function
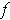 is integrable, and, by the squeeze principle, it has the
desired value.
is integrable, and, by the squeeze principle, it has the
desired value.
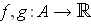 be integrable and suppose
be integrable and suppose
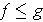 .
Show that
.
Show that
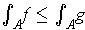 .
.
By Problem 3-3, the function
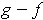 is integrable and
is integrable and
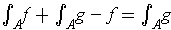 . Using the trivial partition
. Using the trivial partition
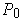 in which
in which
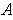 is the only rectangle,
we have
is the only rectangle,
we have
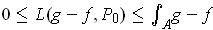 since
since
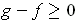 . This proves the
result.
. This proves the
result.
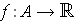 is integrable, show that
is integrable, show that
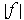 is
integrable and
is
integrable and
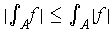 .
.
Consider the function
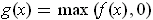 . For any rectangle contained in
. For any rectangle contained in
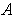 , we have
, we have
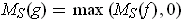 and
and
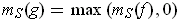 .
If
.
If
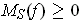 , then
, then
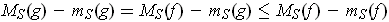 .
On the other hand, if
.
On the other hand, if
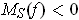 , then
, then
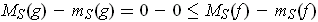 . Let
. Let
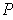 be a partition as in Theorem 3-3 applied to
be a partition as in Theorem 3-3 applied to
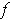 and
and
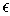 .
Then this implies that
.
Then this implies that
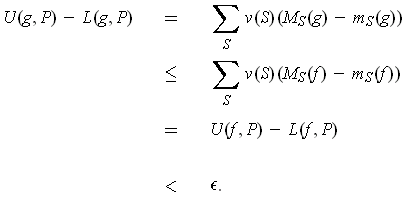
So,
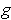 is integrable by Theorem 3-3.
is integrable by Theorem 3-3.
Similarly, one can show that
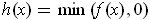 is integrable. But then
by Problem 3-3, it follows that
is integrable. But then
by Problem 3-3, it follows that
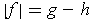 is integrable.
But then, so if
is integrable.
But then, so if
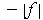 integrable.
Further, since
integrable.
Further, since
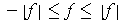 , Problem 3-5 implies that
, Problem 3-5 implies that
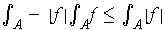 . Since
. Since
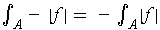 by Problem 3-3 (c),
it follows that
by Problem 3-3 (c),
it follows that
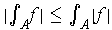 .
.
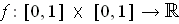 be defined by
be defined by
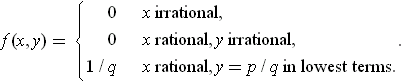
Show that
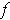 is integrable and
is integrable and
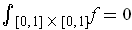 .
.
Let
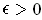 . Choose a positive integer
. Choose a positive integer
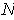 so that
so that
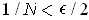 .
Let
.
Let
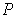 be any partition of
be any partition of
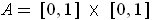 such that every point
such that every point
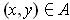 with
with
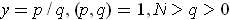 lies in a rectangle of
lies in a rectangle of
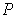 of height
(in the
of height
(in the
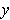 direction) at most
direction) at most
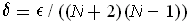 . Since there
are at most
. Since there
are at most
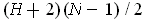 such pairs
such pairs
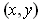 , such a
, such a
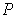 exists and the total
volume of all the rectangles containing points of this type is at most
exists and the total
volume of all the rectangles containing points of this type is at most
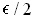 . Since
. Since
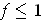 , the contribution to
, the contribution to
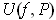 from these
rectangles is also at most
from these
rectangles is also at most
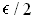 . For the remaining rectangles
. For the remaining rectangles
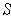 , the
value of
, the
value of
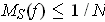 and their total volume is, of course, no larger than
1; so their contribution to
and their total volume is, of course, no larger than
1; so their contribution to
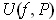 is at most
is at most
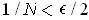 . It
follows that
. It
follows that
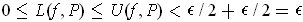 .
By Theorem 3-3,
.
By Theorem 3-3,
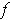 is integrable and the squeeze principle implies that its
integral is 0.
is integrable and the squeeze principle implies that its
integral is 0.