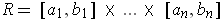 is not
of content 0 if
is not
of content 0 if
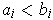 for
for
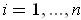 .
.
Suppose
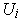 for
for
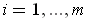 are closed rectangles which form a cover
for
are closed rectangles which form a cover
for
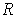 . By replacing the
. By replacing the
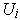 with
with
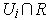 , one can assume that
, one can assume that
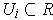 for all
for all
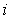 . Let
. Let
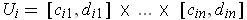 .
Choose a partition
.
Choose a partition
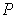 which refines all of the
partitions
which refines all of the
partitions
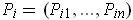 where
where
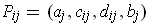 Note that
Note that
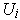 is a rectangle of the cover
is a rectangle of the cover
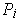 . Let
. Let
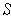 be any rectangle
in
be any rectangle
in
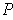 with non-empty interior. Since the intersection of any two rectangles
of a partition is contained in their boundaries, if
with non-empty interior. Since the intersection of any two rectangles
of a partition is contained in their boundaries, if
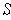 contains an interior
point
contains an interior
point
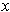 not in
not in
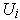 for some
for some
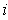 , then
, then
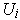 contains only boundary points
of
contains only boundary points
of
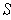 . So, if
. So, if
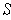 has non-empty interior, then
has non-empty interior, then
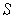 is a subset of
is a subset of
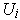 for some
for some
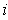 since the union of the
since the union of the
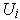 is
is
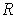 . The sum of the volumes of
the rectangles of
. The sum of the volumes of
the rectangles of
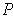 is the volume of
is the volume of
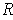 , which is at most equal to the
sum of the volumes of the
, which is at most equal to the
sum of the volumes of the
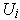 . So
. So
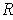 is not of content 0 as it cannot
be covered with rectangles of total area less than the volume of
is not of content 0 as it cannot
be covered with rectangles of total area less than the volume of
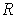 .
.
- Show that an unbounded set
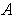 cannot have content 0.
cannot have content 0.
Suppose
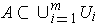 where
where
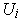 are rectangles, say
are rectangles, say
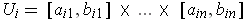 . Let
. Let
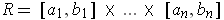 where
where
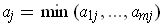 and
and
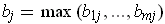 . Then
. Then
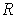 contains all the
contains all the
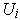 and hence also
and hence also
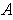 . But then
. But then
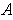 is bounded, contrary to hypothesis.
is bounded, contrary to hypothesis.
- Give an example of a closed set of measure 0 which does not have
content 0.
The set of natural numbers is unbounded, and hence not of content 0 by part (a). On the other hand, it is of measure zero. Indeed, if
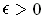 , then
the union of the open intervals
, then
the union of the open intervals
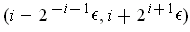 for
for
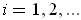 . contains all the natural numbers and the total volume
of all the intervals is
. contains all the natural numbers and the total volume
of all the intervals is
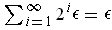 .
.
-
If C is a set of content 0, show that the boundary of
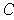 also has
content 0.
also has
content 0.
Suppose a finite set of open rectangles
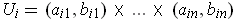 ,
,
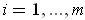 . cover of
. cover of
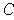 and have total volume
less than
and have total volume
less than
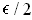 where
where
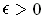 .
Let
.
Let
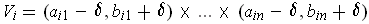 where
where
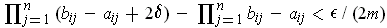 . Then the union of the
. Then the union of the
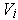 cover the boundary of
cover the boundary of
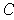 and have total volume less than
and have total volume less than
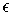 .
So the boundary of
.
So the boundary of
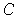 is also of content 0.
is also of content 0.
- Give an example of a bounded set
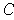 of measure 0 such that the
boundry of
of measure 0 such that the
boundry of
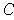 does not have measure 0.
does not have measure 0.
The set of rational numbers in the interval
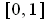 is of measure 0 (cf Proof
of Problem 3-9 (b)), but
its boundary
is of measure 0 (cf Proof
of Problem 3-9 (b)), but
its boundary
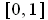 is not of measure 0 (by Theorem 3-6 and Problem 3-8).
is not of measure 0 (by Theorem 3-6 and Problem 3-8).
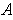 be the set of Problem 1-18. If
be the set of Problem 1-18. If
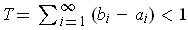 , show that the boundary of
, show that the boundary of
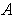 does not have measure 0.
does not have measure 0.
The set
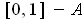 closed and bounded, and hence compact. If it were also
of measure 0, then it would be of content 0 by Theorem 3-6. But then there
is a finite collection of open intervals which cover the set and have total
volume less than
closed and bounded, and hence compact. If it were also
of measure 0, then it would be of content 0 by Theorem 3-6. But then there
is a finite collection of open intervals which cover the set and have total
volume less than
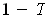 . Since the set these open intervals together with the
set of
. Since the set these open intervals together with the
set of
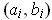 form an open cover of [0, 1], there is a finite subcover
of
form an open cover of [0, 1], there is a finite subcover
of
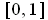 . But then the sum of the lengths of the intervals in this
finite subcover would be less than 1, contrary to Theorem 3-5.
. But then the sum of the lengths of the intervals in this
finite subcover would be less than 1, contrary to Theorem 3-5.
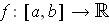 be an increasing function. Show
that
be an increasing function. Show
that
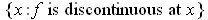 is a set of measure 0.
is a set of measure 0.
Using the hint, we know by Problem 1-30 that the set of
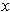 where
where
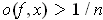 if finite for every
if finite for every
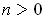 . Hence the set of discontinuities of
. Hence the set of discontinuities of
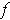 is
a countable union of finite sets, and hence has measure 0 by Theorem 3-4.
is
a countable union of finite sets, and hence has measure 0 by Theorem 3-4.
- Show that the set of all rectangles
 where each
where each
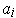 and each
and each
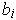 are
rational can be arranged into a sequence (i.e. form a countable set).
are
rational can be arranged into a sequence (i.e. form a countable set).
Since the set of rational numbers is countable, and cartesian products of countable sets are countable, so is the set of all
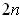 -tuples of rational
numbers. Since the set of these intervals is just a subset of this set,
it must be countable too.
-tuples of rational
numbers. Since the set of these intervals is just a subset of this set,
it must be countable too.
- If
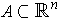 is any set and
is any set and
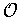 is an open cover
of
is an open cover
of
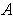 , show that there is a sequence
, show that there is a sequence
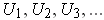 of members of
of members of
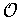 which also cover
which also cover
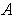 .
.
Following the hint, for each
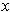 in
in
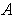 , there is a rectangle B of the type
in part (a) such that
, there is a rectangle B of the type
in part (a) such that
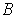 has non-zero volume, contains
has non-zero volume, contains
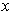 and is contained
in some
and is contained
in some
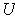 in
in
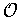 . In fact, we can even assume that
. In fact, we can even assume that
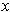 is in the
interior of the rectangle
is in the
interior of the rectangle
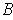 . In particular, the union of the interiors of
the rectangles
. In particular, the union of the interiors of
the rectangles
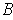 (where
(where
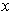 is allowed to range throughout
is allowed to range throughout
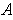 ) is a cover
of
) is a cover
of
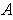 . By part (a), the set of these
. By part (a), the set of these
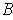 are countable, and hence so are
the set of corresponding
are countable, and hence so are
the set of corresponding
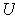 's; this set of corresponding
's; this set of corresponding
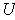 's cover
's cover
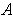 .
.