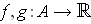 are integrable,
so is
are integrable,
so is
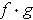 .
.
The set of
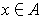 where
where
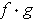 is not continuous is contained in
the union of the sets where
is not continuous is contained in
the union of the sets where
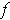 and
and
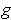 are not continuous. These last two
sets are of measure 0 by Theorem 3-8; so theee first set is also of measure
0. But then
are not continuous. These last two
sets are of measure 0 by Theorem 3-8; so theee first set is also of measure
0. But then
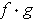 is integrable by Theorem 3-8.
is integrable by Theorem 3-8.
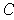 has content 0, then
has content 0, then
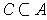 for some closed
rectangle
for some closed
rectangle
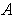 and
and
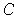 is Jordan-measurable and
is Jordan-measurable and
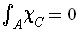 .
.
If
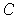 has content 0, then it is bounded by Problem 3-9 (a); so it is a subset
of an closed rectangle
has content 0, then it is bounded by Problem 3-9 (a); so it is a subset
of an closed rectangle
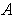 . Since
. Since
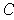 has content 0, one has
has content 0, one has
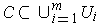 for some open rectangles
for some open rectangles
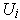 the sum of whose volumes can be made as small
as desired. But then the boundary of
the sum of whose volumes can be made as small
as desired. But then the boundary of
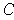 is contained in the closure of
is contained in the closure of
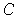 ,
which is contained in the union of the closures of the
,
which is contained in the union of the closures of the
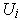 (since this
union is closed). But then the boundary of
(since this
union is closed). But then the boundary of
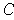 must be of content 0, and
so
must be of content 0, and
so
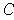 is Jordan measurable by Theorem 3-9. Further, by Problem 3-5, one
has
is Jordan measurable by Theorem 3-9. Further, by Problem 3-5, one
has
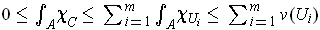 which can be made as small as desired; so
which can be made as small as desired; so
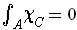 .
.
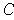 of measure 0 such that
of measure 0 such that
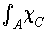 does not exist.
does not exist.
Let
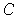 be the set of rational numbers in
be the set of rational numbers in
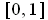 . Then the boundary of
. Then the boundary of
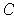 is
is
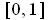 , which is not of measure 0. So
, which is not of measure 0. So
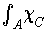 does not exist
by Theorem 3-9.
does not exist
by Theorem 3-9.
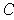 is a bounded set of measure 0 and
is a bounded set of measure 0 and
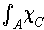 exists,
show that
exists,
show that
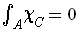 .
.
Using the hint, let
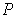 be a partition of
be a partition of
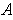 where
where
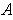 is a closed rectangle
containing
is a closed rectangle
containing
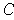 . Then let
. Then let
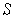 be a rectangle of
be a rectangle of
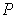 of positive volume.
Then
of positive volume.
Then
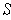 is not of measure 0 by Problem 3-8, and so
is not of measure 0 by Problem 3-8, and so
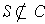 .
But then there is a point of
.
But then there is a point of
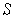 outside of
outside of
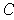 ; so
; so
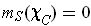 .
Since this is true of all
.
Since this is true of all
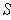 , one has
, one has
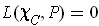 . Since this
holds for all partitions
. Since this
holds for all partitions
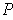 of
of
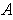 , it follows that
, it follows that
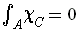 if the integral exists.
if the integral exists.
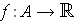 is non-negative and
is non-negative and
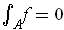 ,
show that
,
show that
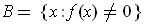 has measure 0.
has measure 0.
Following the hint, let
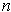 be a positive integer and
be a positive integer and
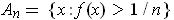 .
Let
.
Let
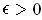 . Let
. Let
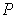 be a partition of
be a partition of
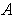 such that
such that
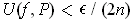 .
Then if
.
Then if
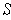 is a rectangle of
is a rectangle of
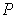 which intersects
which intersects
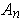 , we have
, we have
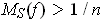 . So
. So
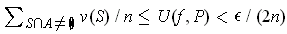 .
By replacing the closed rectangles
.
By replacing the closed rectangles
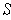 with slightly larger open rectangles,
one gets an open rectangular cover of
with slightly larger open rectangles,
one gets an open rectangular cover of
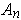 with sets, the sum of whose volumes
is at most
with sets, the sum of whose volumes
is at most
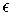 . So
. So
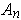 has content 0. Now apply Theorem 3-4 to
conclude that
has content 0. Now apply Theorem 3-4 to
conclude that
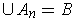 has measure 0.
has measure 0.
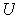 be the open set of Problem 3-11. Show that if
be the open set of Problem 3-11. Show that if
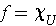 except on a set of measure 0, then f is not integrable on
except on a set of measure 0, then f is not integrable on
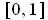 .
.
The set of
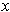 where
where
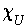 is not continuous is
is not continuous is
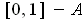 which is not
of measure 0. If the set where
which is not
of measure 0. If the set where
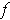 is not continuous is not of measure 0,
then
is not continuous is not of measure 0,
then
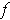 is not integrable by Theorem 3-8. On the other hand, if it
is of measure 0, then taking the union of this set with the set of measure 0
consisting of the points where
is not integrable by Theorem 3-8. On the other hand, if it
is of measure 0, then taking the union of this set with the set of measure 0
consisting of the points where
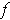 and
and
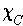 differ gives a set of
measure 0 which contains the set of points where
differ gives a set of
measure 0 which contains the set of points where
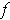 is not continuous. So this
set is also of measure 0, which is a contradiction.
is not continuous. So this
set is also of measure 0, which is a contradiction.
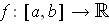 is integrable on
is integrable on
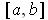 .
.
This is an immediate consequence of Problem 3-12 and Theorem 3-8.
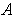 is a closed rectangle, show that
is a closed rectangle, show that
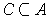 is Jordan
measurable if and only if for every
is Jordan
measurable if and only if for every
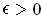 there is a partition
there is a partition
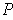 of
of
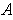 such that
such that
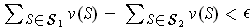 , where
, where
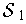 consists of all subrectangles intersecting
consists of all subrectangles intersecting
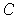 and
and
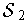 consists of allsubrectangles contained in
consists of allsubrectangles contained in
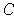 .
.
Suppose
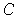 is Jordan measurable. Then its boundary is of content 0 by
Theorem 3-9. Let
is Jordan measurable. Then its boundary is of content 0 by
Theorem 3-9. Let
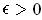 and choose a finite set
and choose a finite set
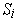 for
for
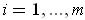 of open rectangles the sum of whose volumes is less than
of open rectangles the sum of whose volumes is less than
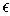 and
such that the
and
such that the
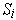 form a cover of the boundary of
form a cover of the boundary of
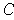 . Let
. Let
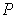 be a
partition of
be a
partition of
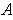 such that every subrectangle of
such that every subrectangle of
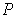 is either contained
within each
is either contained
within each
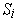 or does not intersect it. This
or does not intersect it. This
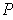 satisfies the
condition in the statement of the problem.
satisfies the
condition in the statement of the problem.
Suppose for every
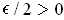 , there is a partition
, there is a partition
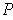 as in the statement.
Then by replacing the rectangles with slightly larger ones, one can obtain
the same result except now one will have
as in the statement.
Then by replacing the rectangles with slightly larger ones, one can obtain
the same result except now one will have
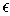 in place of
in place of
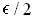 and the
and the
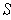 will be open rectangles. This shows that the boundary of
will be open rectangles. This shows that the boundary of
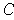 is of content 0; hence
is of content 0; hence
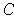 is Jordan measurable by Theorem 3-9.
is Jordan measurable by Theorem 3-9.
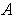 is a Jordan measurable set and
is a Jordan measurable set and
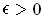 , show that
there is a compact Jordan measurable set
, show that
there is a compact Jordan measurable set
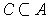 such that
such that
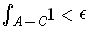 .
.
Let
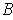 be a closed rectangle containing
be a closed rectangle containing
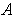 . Apply Problem 3-21 with
. Apply Problem 3-21 with
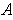 as the Jordan measurable set. Let
as the Jordan measurable set. Let
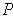 be the partition as in Problem 3-21.
Define
be the partition as in Problem 3-21.
Define
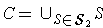 . Then
. Then
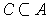 and clearly
and clearly
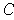 is Jordan measurable by Theorem 3-9. Further
is Jordan measurable by Theorem 3-9. Further
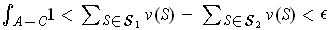 .
.