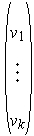
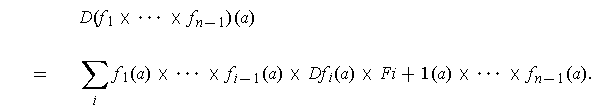be the usual basis of
be the usual basis of
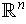 and let
and let
 be the dual basis.
be the dual basis.
- Show that
 . What would the right hand side be if the factor
. What would the right hand side be if the factor
 did not appear in the definition of
did not appear in the definition of
 ?
?
The result is false if the
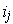 are not distinct; in that case, the value
is zero. Assume therefore that the
are not distinct; in that case, the value
is zero. Assume therefore that the
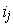 are distinct.
One has using Theorem 4-1(3):
are distinct.
One has using Theorem 4-1(3):
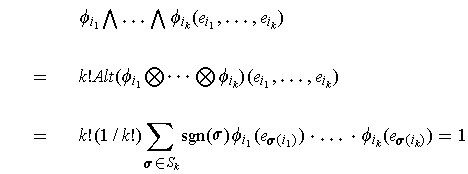
because all the summands except that corresponding to the identity permutation are zero. If the factor were not in the definition of
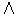 , then the right hand
side would have been
, then the right hand
side would have been
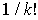 .
.
- Show that
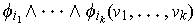 is the determinant of thee
is the determinant of thee
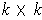 minor of
minor of
 obtained by selecting columns
obtained by selecting columns
 .
.
Assume as in part (a) that the
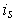 are all distinct.
are all distinct.
A computation similar to that of part (a) shows that
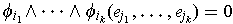 if some
if some
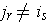 for all
for all
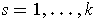 . By multilinearity, it follows that we need only verify
the result when the
. By multilinearity, it follows that we need only verify
the result when the
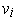 are in the subspace generated by the
are in the subspace generated by the
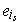 for
for
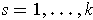 .
.
Consider the linear map
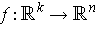 defined by
defined by
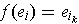 . Then
. Then
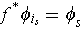 . One has for all
. One has for all
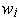 :
:
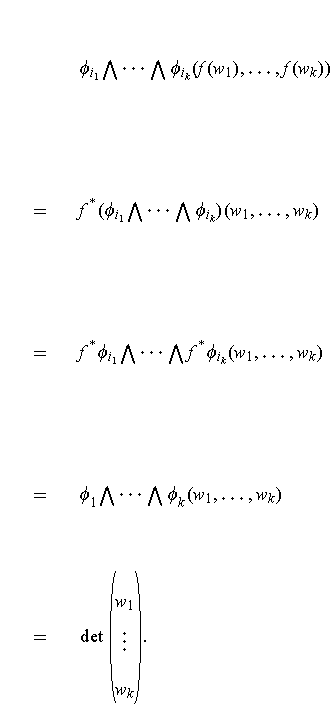
This shows the result.
 is a linear transformation and
is a linear transformation and
 ,
then
,
then
 must be multiplication by
some constant
must be multiplication by
some constant
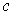 . Show that
. Show that
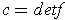 .
.
Let
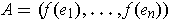 . Then by Theorem 4-6, one has for
. Then by Theorem 4-6, one has for
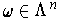 ,
,
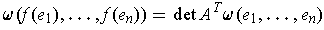 . So
. So
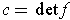 .
.
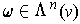 is the volume element determined by
is the volume element determined by
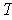 and
and
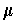 , and
, and
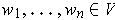 , show that
, show that
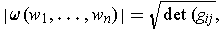
where
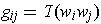 .
.
Let
 be an orthonormal basis for V with respect to
be an orthonormal basis for V with respect to
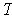 ,
and let
,
and let
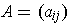 where
where
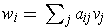 . Then we have
by blinearity:
. Then we have
by blinearity:
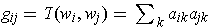 ; the right hand sides
are just the entries of
; the right hand sides
are just the entries of
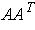 and so
and so
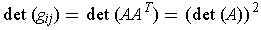 .
By Theorem 4-6,
.
By Theorem 4-6,
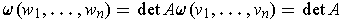 .
Taking absolute values and substituting gives the result.
.
Taking absolute values and substituting gives the result.
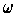 is the volume element of
is the volume element of
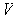 determined by
determined by
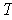 and
and
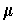 , and
, and
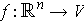 is an isomorphism such that
is an isomorphism such that
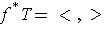 and
such that
and
such that
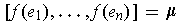 , show that
, show that
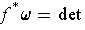 .
.
One has
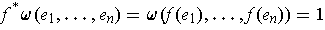 by
the definition of
by
the definition of
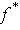 and the fact that
and the fact that
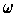 is the volume element
with respect to
is the volume element
with respect to
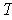 and
and
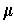 . Further,
. Further,
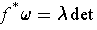 for some
for some
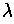 because
because
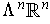 is of dimension 1. Combining, we
have
is of dimension 1. Combining, we
have
 ,
and so
,
and so
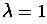 as desired.
as desired.
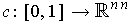 is continuous and each
is continuous and each
 is a basis for
is a basis for
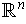 , show that
, show that
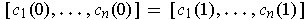 .
.
The function
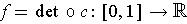 is a continuous function,
whose image does not contain 0 since
is a continuous function,
whose image does not contain 0 since
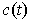 is a basis for every t. By the
intermediate value theorem, it follows that the image of
is a basis for every t. By the
intermediate value theorem, it follows that the image of
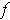 consists of
numbers all of the same sign. So all the
consists of
numbers all of the same sign. So all the
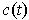 have the same orientation.
have the same orientation.
- If
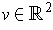 , what is
, what is
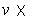 ?
?
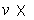 is the cross product of a single vector, i.e. it is the vector
is the cross product of a single vector, i.e. it is the vector
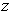 such that
such that
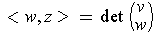 for
every
for
every
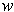 . Substitution shows that
. Substitution shows that
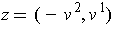 works.
works.
- If
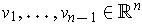 are linearly independent,
show that
are linearly independent,
show that
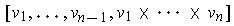 is the usual
orientation of
is the usual
orientation of
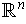 .
.
By the definition, we have
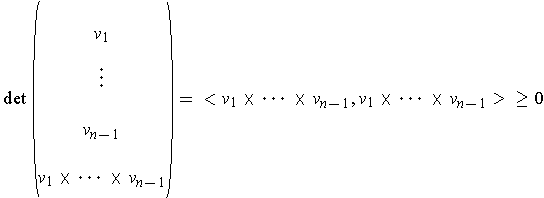 . Since the
. Since the
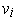 are linearly
independent, the definition of cross product with
are linearly
independent, the definition of cross product with
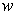 completing the basis
shows that the cross product is not zero. So in fact, the determinant is
positive, which shows the result.
completing the basis
shows that the cross product is not zero. So in fact, the determinant is
positive, which shows the result.
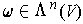 is the volume
element determined by some inner product
is the volume
element determined by some inner product
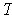 and orientation
and orientation
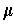 for
for
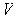 .
.
Let
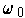 be the volume element determined by some inner product
be the volume element determined by some inner product
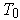 and orientation
and orientation
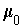 , and let
, and let
 be an orthornormal basis
(with respect to
be an orthornormal basis
(with respect to
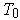 ) such that
) such that
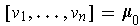 . There is
a scalar
. There is
a scalar
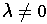 such that
such that
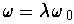 . Let
. Let
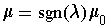 ,
,
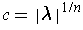 ,
,
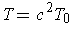 , and
, and
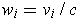 for
for
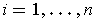 . Then
. Then
 are an orthonormal
basis of
are an orthonormal
basis of
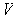 with respect to
with respect to
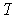 , and
, and
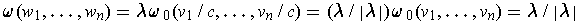 . This shows that
. This shows that
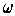 is the volume element of
is the volume element of
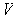 determined by
determined by
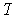 and
and
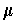 .
.
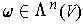 is a volume element, define a
``cross product"
is a volume element, define a
``cross product"
 in terms of
in terms of
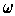 .
.
The cross product is the
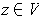 such that
such that
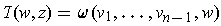 for all
for all
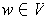 .
.
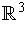 :
:
-
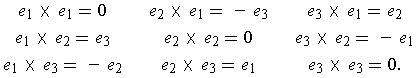
All of these follow immediately from the definition, e.g. To show that
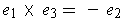 ,
note that
,
note that
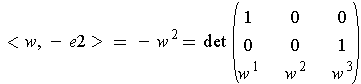 for all
for all
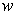 .
.
-
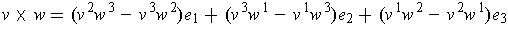 .
.
Expanding out the determinant shows that:
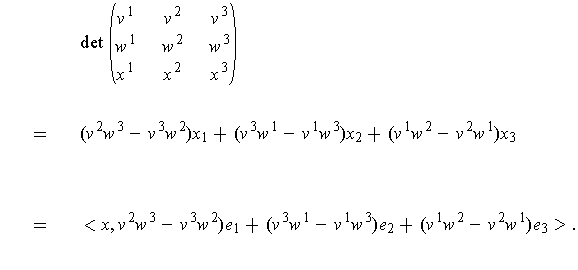
-
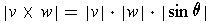 , where
, where
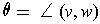 ,
and
,
and
 .
.
The result is true if either
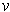 or
or
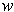 is zero. Suppose that
is zero. Suppose that
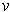 and
and
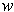 are both non-zero. By Problem 1-8,
are both non-zero. By Problem 1-8,
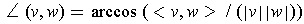 and since
and since
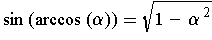 , the first
identity is just
, the first
identity is just
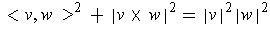 . This is easily
verified by substitution using part (b).
. This is easily
verified by substitution using part (b).
The second assertion follows from the definition since the determinant of a square matrix with two identical rows is zero.
-
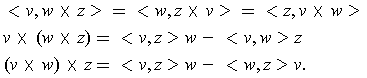
For the first assertion, one has
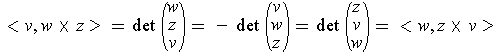 and
and
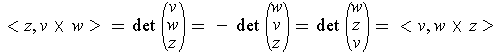 .
.
For the second assertion, one has:
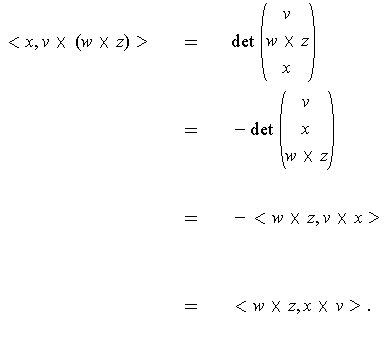
So, one needs to show that
 for all
for all
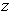 .
But this can be easily verified by expanding everything out using the formula
in part (b).
.
But this can be easily verified by expanding everything out using the formula
in part (b).
The third assertion follows from the second:
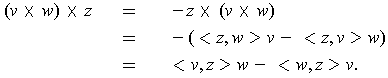
-
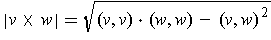 .
.
See the proof of part (c).
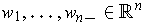 , show that
, show that
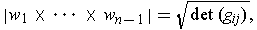
where
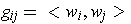 .
.
Using the definition of cross product and Problem 4-3, one has:
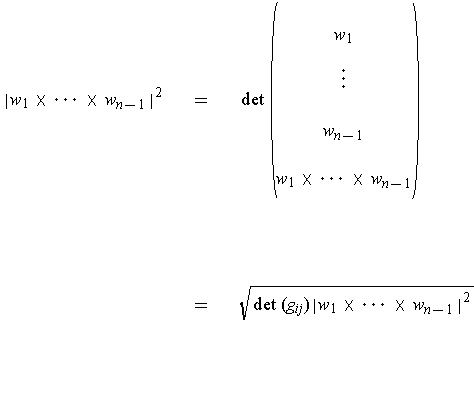
since the matrix
from Problem 4-3 has the form
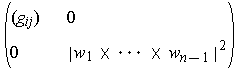 .
This proves the result in the case where
.
This proves the result in the case where
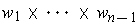 is
not zero. When it is zero, the
is
not zero. When it is zero, the
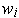 are linearly dependent, and the
bilinearity of inner product imply that
are linearly dependent, and the
bilinearity of inner product imply that
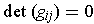 too.
too.
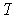 is an inner product on
is an inner product on
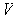 , a linear transformation
, a linear transformation
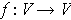 is called self-adjoint (with respect to
is called self-adjoint (with respect to
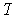 ) if
) if
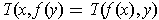 for all
for all
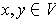 . If
. If
 is an
orthogonal basis and
is an
orthogonal basis and
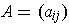 is the matrix of
is the matrix of
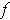 with respect to
this basis, show that
with respect to
this basis, show that
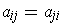 .
.
One has
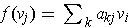 for each
for each
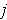 . Using the orthonormality
of the basis, one has:
. Using the orthonormality
of the basis, one has:
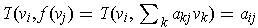 But
But
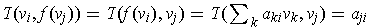 ,
which shows the result.
,
which shows the result.
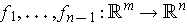 , define
, define
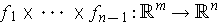 by
by
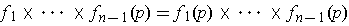 .
Use Problem 2-14 to derive a formula for
.
Use Problem 2-14 to derive a formula for
 when
when
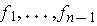 are differentiable.
are differentiable.
Since the cross product is multilinear, one can apply Theorem 2-14 (b) and the chain rule to get: