Exercises: Chapter 4, Section 2

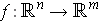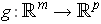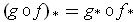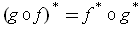    1. If ch4b1.png and ch4b2.png , show that ch4b3.png and ch4b4.png .

      The notation does not fully elucidate the meaning of the assertion. Here is the interpretation:

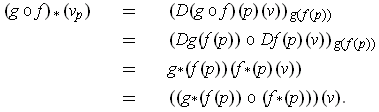
      ch4b5.png

      The second assertion follows from:

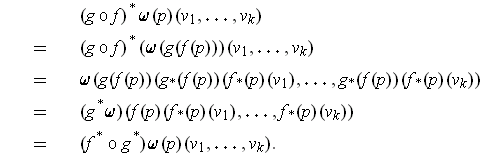
      ch4b6.png

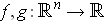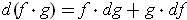    2. If ch4b7.png , show that ch4b8.png .

      One has by the definition and the product rule:

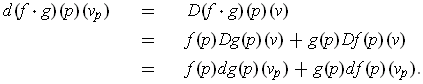
      ch4b9.png

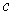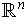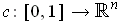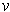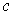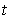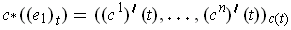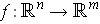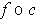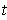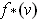  2. Let ch4b10.png be a differentiable curve in ch4b11.png , that is, a differentiable function ch4b12.png . Define the tangent vector ch4b13.png of ch4b14.png at ch4b15.png as ch4b16.png . If ch4b17.png , show that the tangent vector to ch4b18.png at ch4b19.png is ch4b20.png .

    This is an immediate consequence of Problem 4-13 (a).

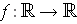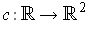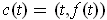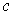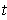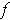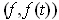  3. Let ch4b21.png and define ch4b22.png by ch4b23.png . Show that the end point of the tangent vector of ch4b24.png at ch4b25.png lies on the tangent line to the graph of ch4b26.png at ch4b27.png .

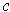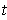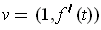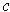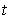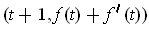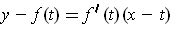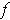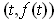    The tangent vector of ch4b28.png at ch4b29.png is ch4b30.png . The end point of the tangent vector of ch4b31.png at ch4b32.png is ch4b33.png which is certainly on the tangent line ch4b34.png to the graph of ch4b35.png at ch4b36.png .

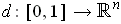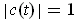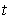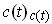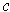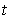  4. Let ch4b37.png be a curve such that ch4b38.png for all ch4b39.png . Show that ch4b40.png and the tangent vector to ch4b41.png at ch4b42.png are perpendicular.

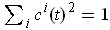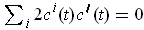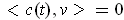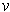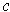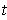    Differentiating ch4b43.png , gives ch4b44.png , i.e. ch4b45.png where ch4b46.png is the tangent vector to ch4b47.png at ch4b48.png .

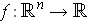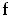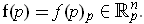
  5. If ch4b49.png , define a vector field ch4b50.png by ch4b51.png
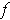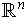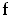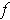    1. Show that every vector field ch4b52.png on ch4b53.png is of the form ch4b54.png for some ch4b55.png .

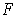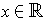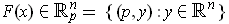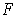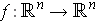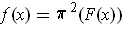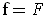      A vector field is just a function ch4b56.png which assigns to each ch4b57.png an element ch4b58.png . Given such an ch4b59.png , define ch4b60.png by ch4b61.png . Then ch4b62.png .

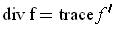    2. Show that ch4b63.png .

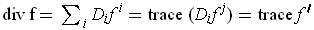      One has ch4b64.png .

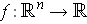  6. If ch4b65.png , define a vector field 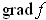ch4b66.png by

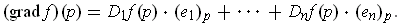
    ch4b67.png

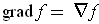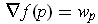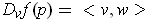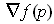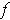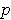    For obvious reasons we also write ch4b68.png . If ch4b69.png , prove that ch4b70.png and conclude that ch4b71.png is the direction in which ch4b72.png is changing fastest at ch4b73.png .

    By Problem 2-29,

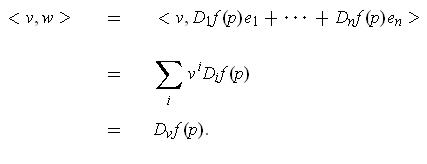
    ch4b74.png

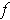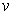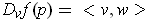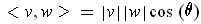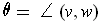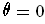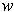    The direction in which ch4b75.png is changing fastest is the direction given by a unit vector ch4b76.png such thatt ch4b77.png is largest possible. Since ch4b78.png where ch4b79.png , this is clearly when ch4b80.png , i.e. in the direction of ch4b81.png .

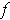  7. If ch4b82.png is a vector field on 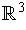ch4b83.png , define the forms

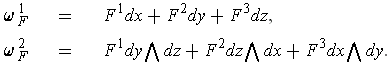
    ch4b84.png

    1. Prove that

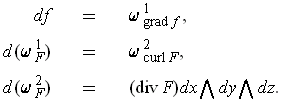
      ch4b85.png

      The first equation is just Theorem 4-7.

      For the second equation, one has:

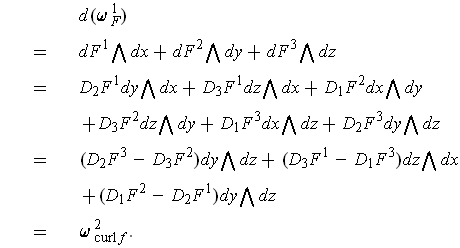
      ch4b86.png

      For the third assertion:

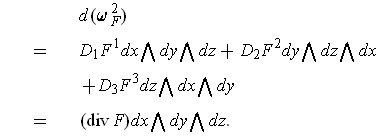
      ch4b87.png

    2. Use (a) to prove that

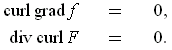
      ch4b88.png

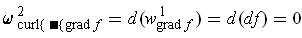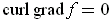      One has ch4b89.png by part (a) and Theorem 4-10 (3); so ch4b90.png .

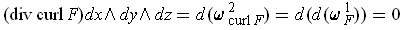      Also, ch4b91.png by part (a) and Theorem 4-10 (3); so the second assertion is also true.

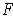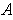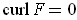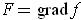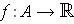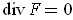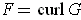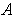    3. If ch4b92.png is a vector field on a star-shaped open set ch4b93.png and ch4b94.png , show that ch4b95.png for some function ch4b96.png . Similarly, if ch4b97.png , show that ch4b98.png for some vector field ch4b99.png on ch4b100.png .

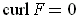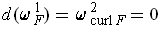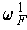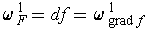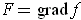      By part (a), if ch4b101.png , then ch4b102.png . By the Theorem 4-11, ch4b103.png is exact, i.e. ch4b104.png . So ch4b105.png .

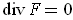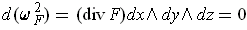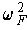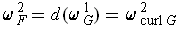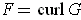      Similarly, if ch4b106.png , then ch4b107.png and so ch4b108.png is closed. By Theorem 4-11, it must then be exact, i.e. ch4b109.png for some ch4b110.png . So ch4b111.png as desired.

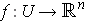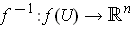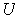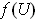  8. Let ch4b112.png be a differentiable function with a differentiable inverse ch4b113.png . If every closed form on ch4b114.png is exact, show that the same is true of ch4b115.png .

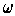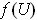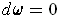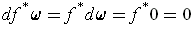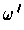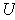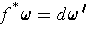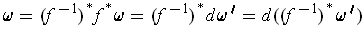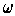    Suppose that the form ch4b116.png on ch4b117.png is closed, i.e. ch4b118.png . Then ch4b119.png and so there is a form ch4b120.png on ch4b121.png such that ch4b122.png . But then ch4b123.png and so ch4b124.png is also exact, as desired.

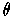  9. Prove that on the set where ch4b125.png is defined, we have

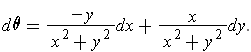
    ch4b126.png

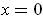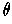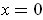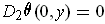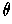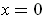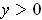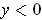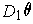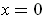    Except when ch4b127.png , the assertion is immediate from the definition of ch4b128.png in Problem 2-41. In case ch4b129.png , one has trivially ch4b130.png because ch4b131.png is constant when ch4b132.png and ch4b133.png (or ch4b134.png ). Further, L'H^{o}pital's Rule allows one to calculate ch4b135.png when ch4b136.png by checking separately for the limit from the left and the limit from the right. 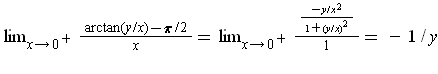For example, ch4b137.png .