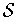 be the set of all singular
be the set of all singular
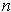 -cubes, and
-cubes, and
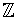 the integers. An
the integers. An
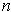 -chain is a function
-chain is a function
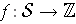 such that
such that
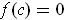 for all but finitely many
for all but finitely many
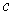 .
Define
.
Define
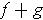 and
and
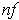 by
by
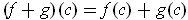 and
and
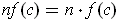 .
Show that
.
Show that
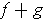 and
and
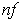 are
are
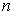 -chains if
-chains if
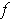 and
and
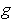 are. If
are. If
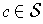 , let
, let
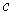 also denote the function
also denote the function
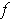 such that
such that
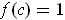 and
and
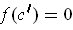 for
for
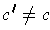 . Show that every
. Show that every
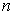 -chain
-chain
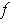 can be
written
can be
written
 for some integers
for some integers
 and singular
and singular
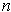 -cubes
-cubes
 .
.
Since
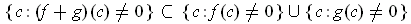 and
and
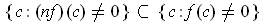 , the functions
, the functions
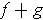 and
and
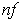 are
are
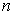 -chains if
-chains if
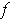 and
and
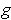 are.
are.
The second assertion is obvious since
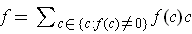 .
.
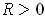 and
and
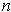 an integer, define the singular 1-cube
an integer, define the singular 1-cube
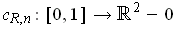 by
by
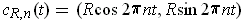 .
Show that there is a singular 2-cube
.
Show that there is a singular 2-cube
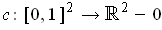 such that
such that
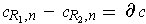 .
.
Define
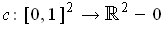 by
by
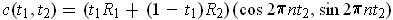 where
where
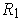 and
and
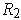 are positive real numbers. The boundary of
are positive real numbers. The boundary of
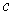 is easily seen to
be
is easily seen to
be
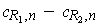 .
.
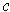 is a singular 1-cube in
is a singular 1-cube in
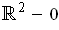 with
with
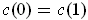 ,
show that there is an integer
,
show that there is an integer
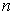 such that
such that
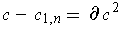 for some
2-chain
for some
2-chain
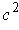 .
.
Given
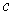 , let
, let
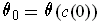 where
where
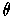 is the function of
Problem 3-41 extended so that it is 0 on the positive
is the function of
Problem 3-41 extended so that it is 0 on the positive
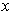 -axis.
Let
-axis.
Let
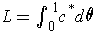 so that
so that
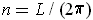 is an integer because
is an integer because
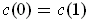 .
Define
.
Define
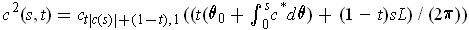 .
One has
.
One has
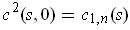 and
and
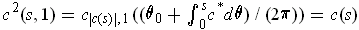 . On the other
boundaries,
. On the other
boundaries,
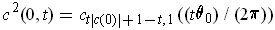 and
and
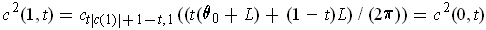 .
So
.
So
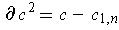 , as desired.
, as desired.