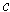 be a singular
be a singular
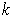 -cube and
-cube and
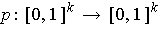 a 1-1 function such that
a 1-1 function such that
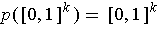 and
and
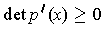 for
for
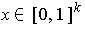 . If
. If
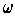 is a
is a
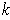 -form, show that
-form, show that
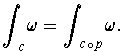
Suppose
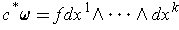 . Using the definition of
the integral, Theorem 4-9, the chain rule, and Theorem 3-13 augmented by
Problem 3-39:
. Using the definition of
the integral, Theorem 4-9, the chain rule, and Theorem 3-13 augmented by
Problem 3-39:
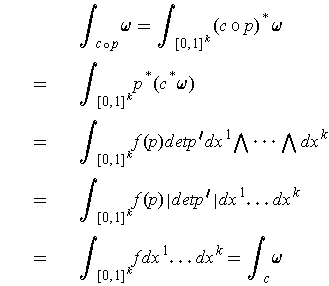
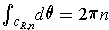 , and use Stokes
Theorem to conclude that
, and use Stokes
Theorem to conclude that
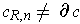 for any 2-chain
for any 2-chain
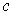 in
in
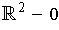 (recall the definition of
(recall the definition of
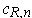 in Problem 4-23).
in Problem 4-23).
One has
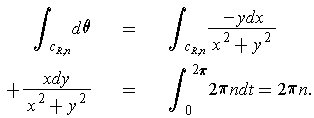
If
 , then Stokes Theorem gives
, then Stokes Theorem gives
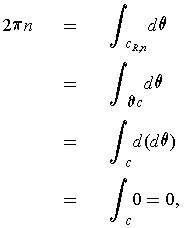
because
 is closed. So
is closed. So
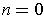 .
.
Note however that no curve is the boundary of any two chain -- as the sum of the coefficients of a boundary is always 0.
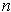 of Problem 4-24 is unique. This integer
is called the winding number of
of Problem 4-24 is unique. This integer
is called the winding number of
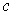 around 0.
around 0.
If
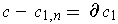 and
and
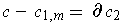 where
where
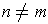 and
and
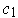 and
and
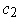 are 2-chains, the letting
are 2-chains, the letting
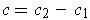 , one has
, one has
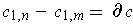 . Using Stokes Theorem, one gets
. Using Stokes Theorem, one gets
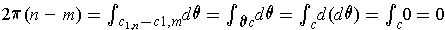 , which is a contradiction.
, which is a contradiction.
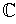 is simply
is simply
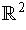 with
with
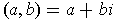 . If
. If
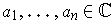 let
let
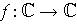 be
be
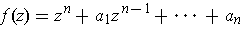 . Define
thee singular 1-cube
. Define
thee singular 1-cube
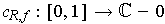 by
by
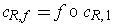 , and the singular 2-cube
, and the singular 2-cube
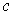 by
by
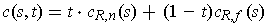 .
.
- Show that
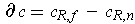 , and that
, and that
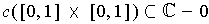 if
if
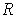 is large enough.
is large enough.
The problem statement is flawed: the author wants
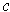 to be defined to
be
to be defined to
be
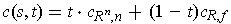 . This would make the
boundary
. This would make the
boundary
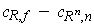 . We assume these changes have been made.
. We assume these changes have been made.
When
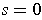 or
or
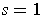 ,
,
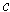 is the curve
is the curve
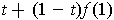 . When
. When
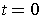 ,
it is the curve
,
it is the curve
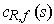 , and when
, and when
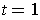 , it is the curve
, it is the curve
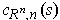 .
So
.
So
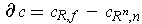 . Let
. Let
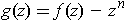 . Then, if
. Then, if
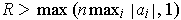 , we have
, we have
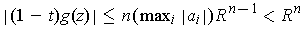 for all
for all
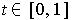 and all
and all
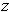 with
with
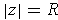 . Since
. Since
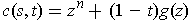 where
where
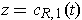 , we see that
, we see that
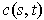 cannot be zero since it is the sum of a number of length
cannot be zero since it is the sum of a number of length
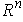 and one which
is smaller in absolute value.
and one which
is smaller in absolute value.
- Using Problem 4-26, prove the Fundamental Theorem of
Algebra: Every polynomial
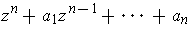 with
with
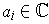 has a root in
has a root in
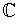 .
.
Suppose that
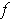 as above has no complex root. Letting
as above has no complex root. Letting
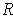 be sufficiently
large, we see by part (a) and Stokes' Theorem that
be sufficiently
large, we see by part (a) and Stokes' Theorem that
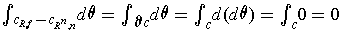 , and
so
, and
so
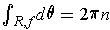 .
.
Now consider the 2-chain
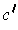 defined by
defined by
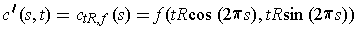 . Now, when
. Now, when
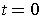 , we get the constant curve
with value
, we get the constant curve
with value
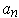 ; when
; when
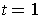 , we get the curve
, we get the curve
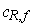 ; and when
; and when
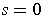 or
or
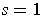 , we get the curve
, we get the curve
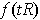 . So the boundary of
. So the boundary of
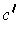 is
is
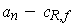 .
Further, we have assumed that
.
Further, we have assumed that
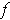 has no complex root, and so
has no complex root, and so
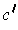 is a
2-chain with values in
is a
2-chain with values in
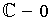 . Again, applying Stokes' Theorem,
we get
. Again, applying Stokes' Theorem,
we get
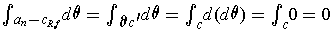 , and so
, and so
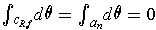 . This contradicts the result of the last paragraph.
. This contradicts the result of the last paragraph.
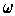 is a 1-form
is a 1-form
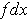 on
on
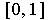 with
with
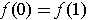 , show
that theere is a unique number
, show
that theere is a unique number
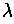 such that
such that
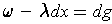 for some function
for some function
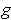 with
with
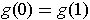 .
.
Following the hint,
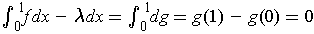 implies
implies
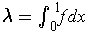 and so
and so
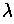 is unique. On the other
hand, if we let
is unique. On the other
hand, if we let
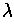 be this value and
be this value and
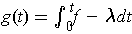 ,
then
,
then
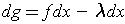 and
and
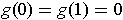 .
.
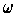 is a 1-form on
is a 1-form on
 such that
such that
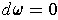 ,
prove that
,
prove that
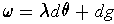
for some
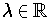 and
and
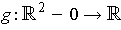 .
The differential
.
The differential
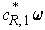 is of the type considered in the last
problem. So there is a unique
is of the type considered in the last
problem. So there is a unique
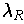 for which there is a
for which there is a
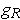 such that
such that
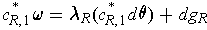 .
.
For positive
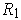 and
and
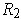 , define the singular 2-cube
, define the singular 2-cube
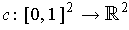 by
by
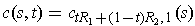 . By Stokes' Theorem, we have
. By Stokes' Theorem, we have
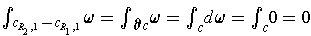 . So
. So
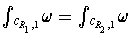 .
By the proof of the last problem, it follows that
.
By the proof of the last problem, it follows that
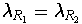 . Henceforth, let
. Henceforth, let
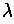 denote this common value.
Note that
denote this common value.
Note that
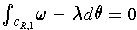 ; and in particular,
; and in particular,
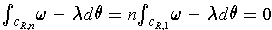 .
.
Let
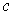 be a singular 1-cube with
be a singular 1-cube with
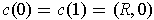 . By Problem 4-24,
there is a 2-chain
. By Problem 4-24,
there is a 2-chain
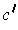 and an
and an
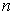 such that
such that
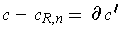 .
By Stokes' Theorem,
.
By Stokes' Theorem,
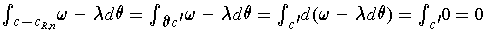 . So
. So
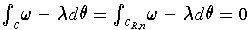 .
.
From the result of the last paragraph, integrating
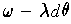 is independent of path. In fact, if you have two singular 1-cubes
is independent of path. In fact, if you have two singular 1-cubes
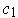 and
and
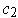 with
with
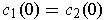 and
and
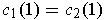 , then prepend a
curve from (1,0) to
, then prepend a
curve from (1,0) to
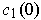 and postpend a path from
and postpend a path from
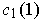 to (1,0) to
get two paths as in the last paragraph. The two integrals are both 0, and
so the integrals over
to (1,0) to
get two paths as in the last paragraph. The two integrals are both 0, and
so the integrals over
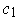 and
and
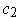 are equal.
are equal.
Now the result follows from Problem 4-32 below.
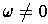 , show that there is a chain
, show that there is a chain
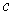 such that
such that
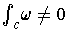 . Use this fact, Stokes' theorem and
. Use this fact, Stokes' theorem and
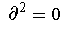 to
prove
to
prove
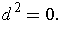
One has
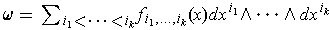 .
Suppose
.
Suppose
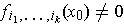 for some
for some
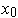 and some choice of
and some choice of
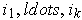 . Then
. Then
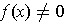 in a closed rectangle of positive
volume centered at
in a closed rectangle of positive
volume centered at
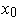 . Take for
. Take for
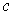 the k-cube defined in an obvious way so that its image
is the part of the closed rectangle with
the k-cube defined in an obvious way so that its image
is the part of the closed rectangle with
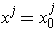 for all
for all
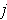 different
from the
different
from the
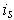 for
for
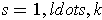 . Then
. Then
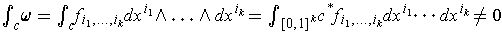 since the integrand is continuous and of the same sign throughout the
region of integration.
since the integrand is continuous and of the same sign throughout the
region of integration.
Suppose
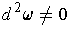 . Let
. Let
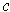 be a chain such that
be a chain such that
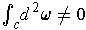 .
By Stokes' Theorem, we would have:
.
By Stokes' Theorem, we would have:
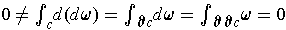 because
because
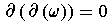 . This is a contradiction.
. This is a contradiction.
- Let
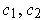 be singular 1-cubes in
be singular 1-cubes in
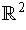 with
with
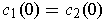 and
and
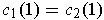 . Show that there is a singular 2-cube
. Show that there is a singular 2-cube
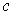 such
that
such
that
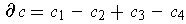 , where
, where
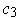 and
and
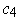 are
degenerate, that is,
are
degenerate, that is,
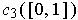 and
and
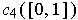 are points. Conclude
that
are points. Conclude
that
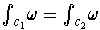 if
if
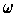 is exact.
Give a counter-example on
is exact.
Give a counter-example on
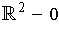 if
if
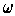 is merely closed.
is merely closed.
Let
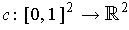 be defined by
be defined by
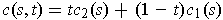 .
Then
.
Then
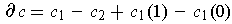 where
where
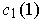 is the curve with
constant value
is the curve with
constant value
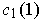 and similarly for
and similarly for
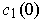 .
.
Suppose
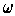 is exact, and hence closed. Then by Stokes' Theorem, we have
is exact, and hence closed. Then by Stokes' Theorem, we have
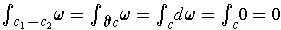 (since
(since
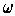 is closed), and so
is closed), and so
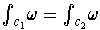 .
.
The example:
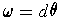 ,
,
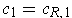 , and
, and
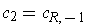 shows that there is no independence of path in
shows that there is no independence of path in
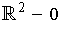 for closed
forms.
for closed
forms.
- If
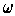 is a 1-form on a subset of
is a 1-form on a subset of
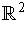 and
and
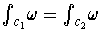 for all
for all
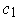 and
and
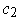 with
with
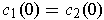 and
and
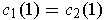 , show that
, show that
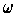 is exact.
is exact.
Although it is not stated, we assume that the subset is open. Further, by treating each component separately, we assume that the subset is pathwise connected.
Fix a point
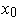 in the subset. For every
in the subset. For every
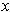 in the set, let
in the set, let
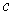 be any
curve from
be any
curve from
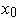 to
to
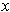 , and set
, and set
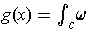 . Because of
independence of path,
. Because of
independence of path,
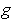 is well defined. Now, if
is well defined. Now, if
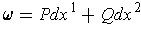 ,
then because
,
then because
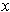 is in the interior of the subset, we can assume that
is in the interior of the subset, we can assume that
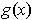 is calculated with a path that ends in a segment with
is calculated with a path that ends in a segment with
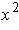 constant.
Clearly, then
constant.
Clearly, then
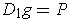 . Similarly,
. Similarly,
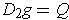 . Note that because
. Note that because
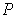 and
and
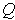 are continuously differentible, it follows that
are continuously differentible, it follows that
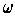 is closed
since
is closed
since
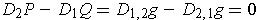 .
.
We want to check differentiability of
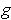 . One has
. One has
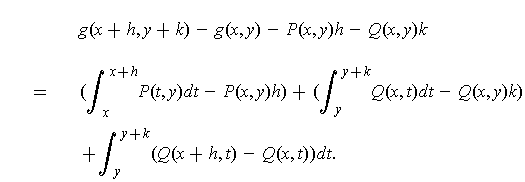
The first pair of terms is
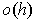 because
because
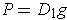 ; similarly the second pair
of terms is
; similarly the second pair
of terms is
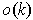 . Finally, continuity of
. Finally, continuity of
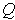 implies that the integrand
is
implies that the integrand
is
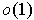 , and so the last integral is also
, and so the last integral is also
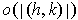 . So
. So
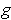 is
differentiable at
is
differentiable at
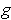 . This establishes the assertion.
. This establishes the assertion.
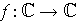 , define
, define
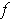 to be differentiable at
to be differentiable at
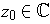 if the limit
if the limit
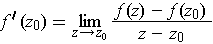
exists. (This quotient involves two complex numbers and this definition is
completely different from the one in Chapter 2.) If
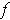 is differeentiable at every
point
is differeentiable at every
point
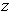 in an open set
in an open set
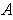 and
and
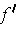 is continuous on
is continuous on
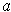 , then
, then
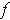 is called
analytic on
is called
analytic on
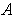 .
.
- Show that
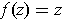 is analytic and
is analytic and
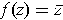 is not (where
is not (where
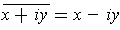 ). Show that the sum, product, and quotient of
analytic functions are analytic.
). Show that the sum, product, and quotient of
analytic functions are analytic.
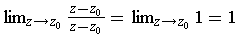 and so
and so
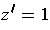 . On the other hand,
. On the other hand,
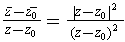 does not have a limit as
does not have a limit as
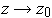 because
because
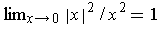 , but
, but
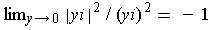 .
.
It is straightforward to check that the complex addition, subtraction, multiplication, and division operations are continuous (except when the quotient is zero). The assertion that being analytic is preserved under these operations as well as the formulas for the derivatives are then obvious, if you use the identities:
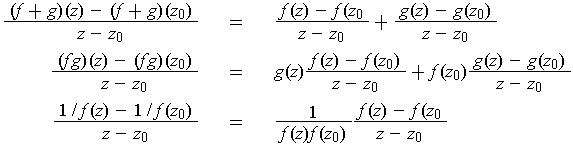
- If
 is analytic on
is analytic on
 , show that
, show that
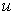 and
and
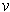 satisfy
the Cauchy-Riemann} equations:
satisfy
the Cauchy-Riemann} equations:
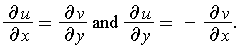
(The converse is also true, if
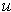 and
and
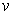 are continuously differentiable;
this is more difficult to prove.)
are continuously differentiable;
this is more difficult to prove.)
Following the hint, we must have:
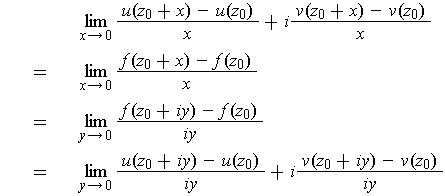
Comparing the real and imaginary parts gives the Cauchy-Riemann equations.
- Let
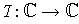 be a linear transformation
(where
be a linear transformation
(where
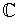 is considered as a vector space over
is considered as a vector space over
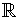 ). If the
matrix of
). If the
matrix of
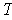 with respect to the basis
with respect to the basis
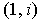 is
is
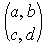 , show that
, show that
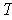 is multiplication by a complex
number if and only if
is multiplication by a complex
number if and only if
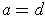 and
and
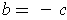 . Part (b) shows that an analytic
function
. Part (b) shows that an analytic
function
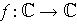 , considered as a function
, considered as a function
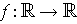 , has a derivative
, has a derivative
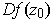 which is multiplication by
a complex number. What complex number is this?
which is multiplication by
a complex number. What complex number is this?
Comparing
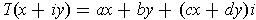 and
and
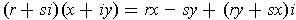 gives
gives
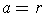 ,
,
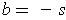 ,
,
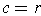 , and
, and
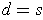 . So,
. So,
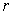 and
and
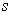 exist if and only if
exist if and only if
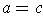 and
and
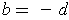 .
.
From the last paragraph, the complex number is
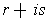 where
where
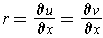 and
and
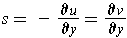 .
.
- Define
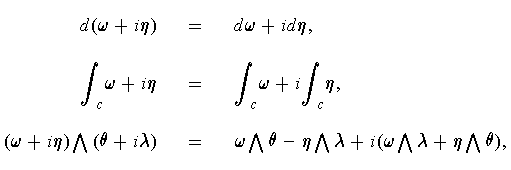
and
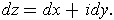
Show that
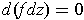 if and only if
if and only if
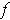 satisfies the
Cauchy-Riemann equations.
satisfies the
Cauchy-Riemann equations.
One has for
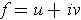 that
that
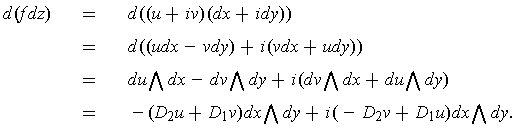
Clearly this is zero if and only if the Cauchy-Riemann equations hold true for
 .
.
- Prove the Cauchy Integral Theorem: If
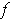 is analytic in
is analytic in
 ,
then
,
then
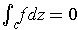 for every closed curve
for every closed curve
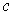 (singular 1-cube with
(singular 1-cube with
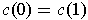 ) such that
) such that
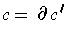 for some 2-chain
for some 2-chain
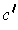 in
in
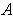 .
.
By parts (b) and (d), the 1-form
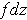 is closed. By Stokes' Theorem,
it follows that
is closed. By Stokes' Theorem,
it follows that
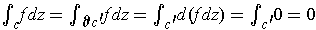 .
.
- Show that if
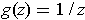 , then
, then
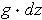 (or
(or
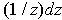 in
classical notation) equals
in
classical notation) equals
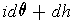 for some function
for some function
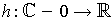 . Conclude that
. Conclude that
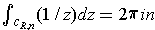 .
.
One has
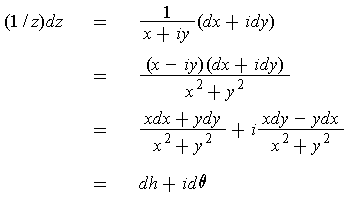
if
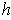 is defined by
is defined by
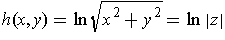 .
.
This then gives
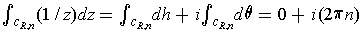 .
.
- If
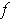 is analytic on
is analytic on
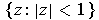 , use the fact that
, use the fact that
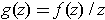 is analytic in
is analytic in
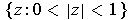 to show that
to show that
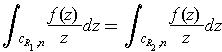
if
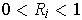 for
for
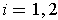 . Use (f) to evaluate
. Use (f) to evaluate
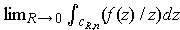 and conclude:
and conclude:
Cauchy Integral Formula: If
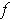 is analytic on
is analytic on
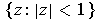 and
and
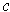 is a closed curve in
is a closed curve in
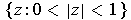 with winding number
with winding number
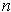 around 0, then
around 0, then
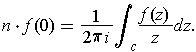
The first assertion follows from part (e) applied to the singular 2-cube
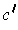 defined by
defined by
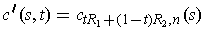 .
.
By a trivial modification of Problem 4-24 (to use
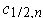 ) and
Stokes' Theorem,
) and
Stokes' Theorem,
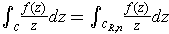 for
for
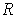 with
with
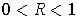 .
.
Further,
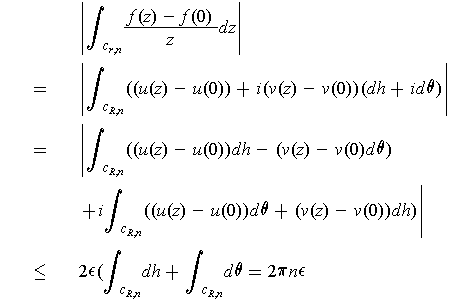
if
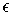 is chosen so that
is chosen so that
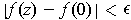 for all
for all
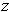 with
with
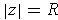 . It follows that
. It follows that
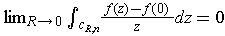 .
Using part (f), we conclude that
.
Using part (f), we conclude that
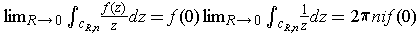 .
The Cauchy integral formula follows from this and the result of the last
paragraph.
.
The Cauchy integral formula follows from this and the result of the last
paragraph.
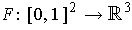 and
and
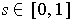 , define
, define
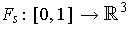 by
by
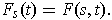 If each
If each
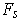 is
a closed curve,
is
a closed curve,
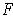 is called a homotopy between the closed curve
is called a homotopy between the closed curve
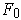 and the closed curve
and the closed curve
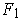 . Suppose
. Suppose
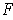 and
and
 are homotopies of
closed curves; if for each
are homotopies of
closed curves; if for each
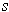 the closed curves
the closed curves
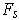 and
and
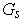 do not intersect, the pair
do not intersect, the pair
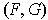 is called a homotopy
between the non-intersecting closed curves
is called a homotopy
between the non-intersecting closed curves
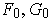 and
and
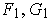 . It
is intuitively obvious that there is no such homotopy with
. It
is intuitively obvious that there is no such homotopy with
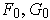 the pair
of curves shown in Figure 4-6 (a), and
the pair
of curves shown in Figure 4-6 (a), and
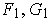 the pair of (b) or (c). The
present problem, and Problem 5-33 prove this for (b) but the proof for (c)
requires different techniques.
the pair of (b) or (c). The
present problem, and Problem 5-33 prove this for (b) but the proof for (c)
requires different techniques.
- If
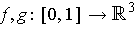 are nonintersecting closed
curves, define
are nonintersecting closed
curves, define
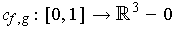 by
by
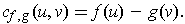
If
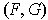 is a homotopy of nonintersecting closed curves define
is a homotopy of nonintersecting closed curves define
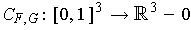 by
by
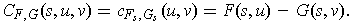
Show that
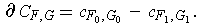
When
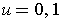 , one gets the same singular 2-cube
, one gets the same singular 2-cube
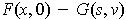 ;
similarly, when
;
similarly, when
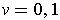 , one gets the same singular 2-cube
, one gets the same singular 2-cube
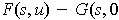 .
When
.
When
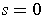 (respectively
(respectively
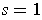 ), one gets the singular 2-cube
), one gets the singular 2-cube
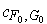 (respectively
(respectively
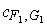 ). So
). So
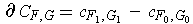 which agrees with the assertion only up to a sign.
which agrees with the assertion only up to a sign.
- If
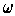 is a closed 2-form on
is a closed 2-form on
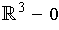 , show that
, show that
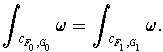
By Stokes' Theorem and part (a), one has
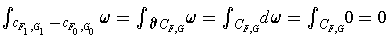 .
.