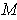 is a
is a
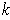 -dimensional manifold with boundary, prove that
-dimensional manifold with boundary, prove that
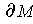 is a
is a
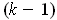 -dimensional manifold and
-dimensional manifold and
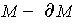 is a
is a
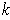 =dimensional manifold.
=dimensional manifold.
The boundary of
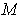 is the set of points
is the set of points
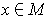 which satisfy condition
which satisfy condition
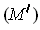 . Let
. Let
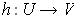 be as in condition
be as in condition
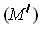 ; then the same
; then the same
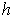 works for every point in
works for every point in
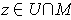 such that
such that
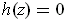 . In
particular, each such
. In
particular, each such
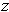 is in
is in
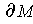 . Further,
. Further,
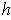 also is map
which shows that condition
also is map
which shows that condition
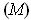 is satisfied for each such
is satisfied for each such
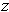 . So
. So
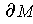 is a manifold of dimension
is a manifold of dimension
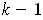 , and because those points which don't satisfy
, and because those points which don't satisfy
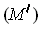 must satisfy
must satisfy
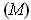 , it follows that
, it follows that
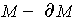 is a manifold of
dimension
is a manifold of
dimension
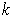 .
.
Following the hint, consider
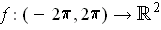 defined by
defined by
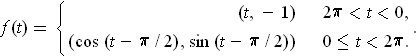
Let
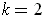 ,
,
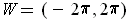 ,
,
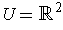 ,
,
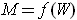 . Then condition
. Then condition
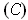 holds except for part (3) since
holds except for part (3) since
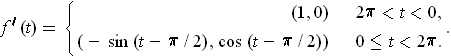
- Let
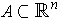 be an open set such that boundary
be an open set such that boundary
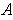 is an
is an
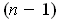 -dimensional manifold. Show that
-dimensional manifold. Show that
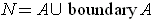 is an
is an
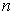 -dimensional manifold with boundary. (It is well to bear in mind
the following example: if
-dimensional manifold with boundary. (It is well to bear in mind
the following example: if
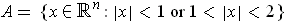 ,
then
,
then
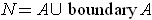 is a manifold with boundary, but
is a manifold with boundary, but
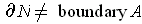 .)
.)
Since
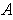 is open, each of its points satisfies condition
is open, each of its points satisfies condition
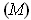 with
with
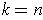 .
Let
.
Let
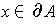 . Then
. Then
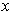 satisfies
satisfies
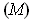 with
with
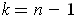 , say with
the function
, say with
the function
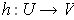 . Let
. Let
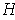 be one of the half-planes
be one of the half-planes
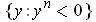 or
or
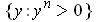 Suppose there is a sequence
Suppose there is a sequence
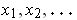 of points of
of points of
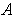 such that the
such that the
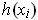 all lie in
all lie in
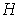 and converge to
and converge to
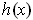 . If there is no open neighborhood
. If there is no open neighborhood
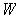 of
of
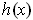 such that
such that
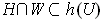 , then there is a sequence
, then there is a sequence
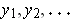 of points
of
of points
of
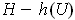 such that the sequence converges to
such that the sequence converges to
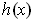 . But then
the line segments from
. But then
the line segments from
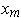 to
to
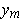 must contain a point o the boundary
of
must contain a point o the boundary
of
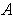 , which is absurd since the points of U in the boundary of
, which is absurd since the points of U in the boundary of
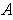 all
map to points with last coordinate 0. It follows that h restricted to
an appropriately small open subset of
all
map to points with last coordinate 0. It follows that h restricted to
an appropriately small open subset of
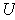 either satisfies condition
either satisfies condition
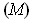 or condition
or condition
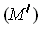 . This proves the assertion.
. This proves the assertion.
- Prove a similar assertion for an open subset of an n-dimensional
manifold.
The generalization to manifolds is proved in the same way, except you need to restrict attention to a coordinate system around
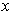 . By working in
the set
. By working in
the set
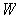 of condition
of condition
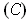 , one gets back into the case where one is
contained within
, one gets back into the case where one is
contained within
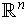 , and the same argument applies.
, and the same argument applies.
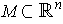 is a
is a
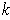 -dimensional manifold and
-dimensional manifold and
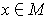 , then there is an open set
, then there is an open set
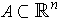 containing
containing
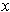 and a differentiable function
and a differentiable function
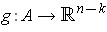 such that
such that
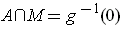 and
and
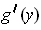 has rank
has rank
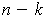 when
when
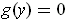 .
.
Let
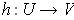 be as in condition
be as in condition
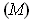 applied to
applied to
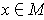 ,
,
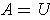 ,
and
,
and
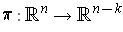 be defined by
be defined by
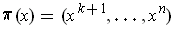 .
Then the function
.
Then the function
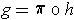 satisfies all the desired conditions.
satisfies all the desired conditions.
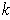 -dimensional (vector) subspace of
-dimensional (vector) subspace of
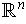 is a
is a
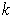 -dimensional manifold.
-dimensional manifold.
Let
 be a basis for the subspace, and choose
be a basis for the subspace, and choose
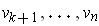 so that all the
so that all the
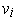 together form a basis for
together form a basis for
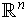 . Define a
map
. Define a
map
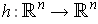 by
by
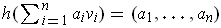 . One can verify that
. One can verify that
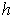 satisfies the condition
satisfies the condition
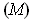 .
.
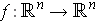 , the graph of
, the graph of
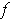 is
is
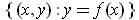 . Show that the graph of
. Show that the graph of
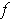 is an
is an
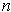 -dimensional manifold if and only if
-dimensional manifold if and only if
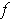 is differentiable.
is differentiable.
If
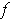 is differentiable, the map
is differentiable, the map
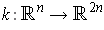 defined by
defined by
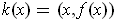 is easily verified to be a coordinate
system around all points of the graph of f; so the graph is a manifold of
dimension n.
is easily verified to be a coordinate
system around all points of the graph of f; so the graph is a manifold of
dimension n.
Conversely, suppose
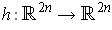 is as in
condition
is as in
condition
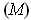 for some point
for some point
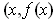 in the graph. Let
in the graph. Let
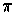 be
the projection on the last
be
the projection on the last
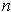 coordinates. Then apply the Implicit function
theorem to
coordinates. Then apply the Implicit function
theorem to
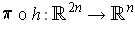 . The differentiable
function
. The differentiable
function
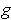 obtained from this theorem must be none other than
obtained from this theorem must be none other than
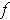 since
the graph is the set of points which map to zero by
since
the graph is the set of points which map to zero by
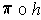 .
.
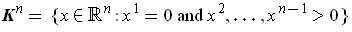 .
If
.
If
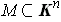 is a
is a
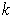 -dimensional manifold and
-dimensional manifold and
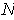 is obtained by
revolving
is obtained by
revolving
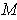 around the axis
around the axis
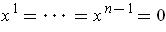 , show that
, show that
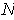 is
a
is
a
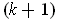 -dimensional manifold. Example: the torus (Figure 5-4).
-dimensional manifold. Example: the torus (Figure 5-4).
Consider the case where n = 3. If
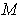 is defined in some open set by
is defined in some open set by
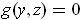 , then
, then
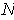 is defined by
is defined by
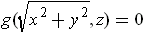 . The Jacobian
is
. The Jacobian
is
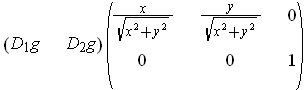 Since either
Since either
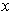 or
or
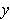 is non-zero, it is easy to see that the Jacobian
has the proper rank.
is non-zero, it is easy to see that the Jacobian
has the proper rank.
In the case where n > 3, it is not obvious what one means by ``rotate".
- If
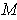 is a
is a
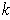 -dimensional manifold in
-dimensional manifold in
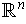 and
and
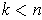 ,
show that
,
show that
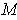 has measure 0.
has measure 0.
For each
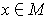 , one has condition
, one has condition
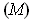 holding for some function
holding for some function
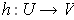 . Let
. Let
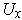 be the domain of one of these functions, where
we can choose
be the domain of one of these functions, where
we can choose
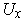 to be a ball with center at rational coordinates and
rational radius. Then
to be a ball with center at rational coordinates and
rational radius. Then
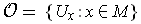 is a countable
cover of
is a countable
cover of
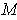 . Now each
. Now each
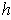 maps points of
maps points of
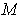 in
in
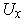 to points with
the last
to points with
the last
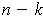 coordinates 0. Take a thin plate including the image of
coordinates 0. Take a thin plate including the image of
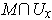 ; its inverse image has volume which can be bounded by
; its inverse image has volume which can be bounded by
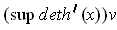 where
where
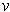 is the volume of the plate (by the change of
variables formula). By choosing the thickness of the plate sufficiently
small, we can guarantee that this value is no more than
is the volume of the plate (by the change of
variables formula). By choosing the thickness of the plate sufficiently
small, we can guarantee that this value is no more than
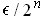 for the
for the
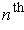 element of the cover. This shows the result.
element of the cover. This shows the result.
- If
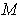 is a closed
is a closed
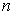 -dimensional manifold with boundary in
-dimensional manifold with boundary in
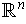 , show that the boundary of
, show that the boundary of
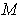 is
is
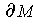 . Give a
counter-example if
. Give a
counter-example if
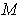 is not closed.
is not closed.
Clearly, every element of
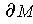 is in the boundary of
is in the boundary of
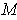 by the
condition
by the
condition
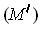 . If
. If
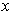 is in the boundary of
is in the boundary of
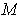 , then
, then
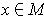 since
since
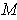 is closed. So if
is closed. So if
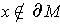 , it must satisfy condition
, it must satisfy condition
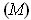 .
But then
.
But then
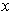 is in the interior of
is in the interior of
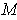 because the dimension of
because the dimension of
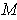 is n.
is n.
The open unit interval in
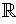 is a counter-example if we do not
require
is a counter-example if we do not
require
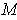 to be closed.
to be closed.
- If
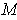 is a compact
is a compact
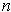 -dimensional manifold with boundary in
-dimensional manifold with boundary in
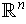 ,
show that
,
show that
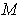 is Jordan-measurable.
is Jordan-measurable.
By part (b), the boundary of
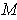 is
is
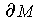 . By Problem 5-1,
. By Problem 5-1,
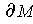 is an
is an
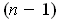 -dimensional manifold contained in
-dimensional manifold contained in
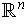 . By part (a),
it follows that
. By part (a),
it follows that
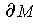 is of measure 0. Finally, since
is of measure 0. Finally, since
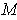 is bounded,
the definition of Jordan measurable is satisfied.
is bounded,
the definition of Jordan measurable is satisfied.