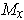 consists of the tangent vectors at
consists of the tangent vectors at
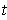 of curves
of curves
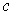 in
in
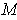 with
with
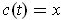 .
.
Let
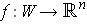 be a coordinate system around
be a coordinate system around
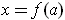 in
in
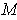 ; by
replace
; by
replace
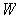 with a subset, one can assume that
with a subset, one can assume that
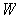 is a rectangle centered
at
is a rectangle centered
at
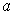 . For
. For
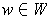 and
and
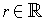 , let
, let
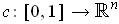 be
the curve
be
the curve
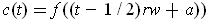 . Then
. Then
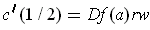 ranges through
out
ranges through
out
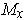 as
as
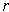 and
and
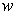 vary.
vary.
Conversely, suppose that
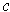 is a curve in
is a curve in
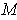 with
with
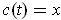 . Then let
. Then let
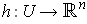 be as in condition
be as in condition
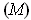 for the point
for the point
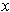 .
We know by the proof of Theorem 5-2, that
.
We know by the proof of Theorem 5-2, that
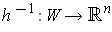 is
a coordinate system about
is
a coordinate system about
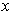 where
where
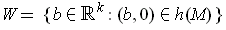 .
Since
.
Since
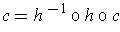 , it follows that the tangent vector of
, it follows that the tangent vector of
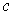 is in
is in
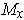 .
.
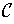 is a collection of coordinate systems for
is a collection of coordinate systems for
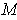 such that (1) For each
such that (1) For each
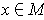 there is
there is
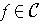 which is
a coordinate system around
which is
a coordinate system around
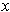 ; (2) if
; (2) if
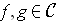 , then
, then
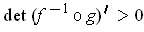 . Show that there is a unique orientation of
. Show that there is a unique orientation of
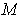 such that
such that
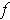 is orientation-preserving for all
is orientation-preserving for all
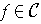 .
.
Define the orientation to be the
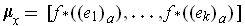 for every
for every
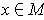 ,
,
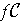 , and
, and
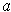 with
with
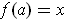 . In order for
this to be well defined, we must show that we get the same orientation
if we use use
. In order for
this to be well defined, we must show that we get the same orientation
if we use use
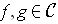 and
and
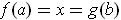 . But
analogous to the author's observation of p. 119, we know that
. But
analogous to the author's observation of p. 119, we know that
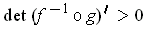 implies that
implies that
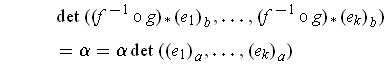
where
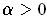 . Let
. Let
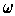 be such that
be such that
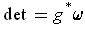 .
Then we have
.
Then we have
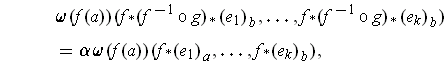
i.e.
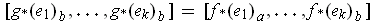 as desired.
as desired.
Clearly, the definition makes
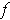 orientation preserving for all
orientation preserving for all
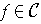 ,
and this is only orientation which could satisfy this condition.
,
and this is only orientation which could satisfy this condition.
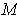 is an
is an
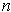 -dimensional manifold-with-boundary in
-dimensional manifold-with-boundary in
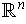 ,
define
,
define
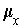 as the usual orientation of
as the usual orientation of
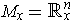 (the orientation
(the orientation
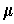 so defined is the usual orientation of
so defined is the usual orientation of
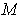 . If
. If
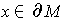 ,
show that the two definitions of
,
show that the two definitions of
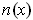 given above agree.
given above agree.
Let
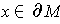 and
and
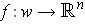 be a coordinate system
about
be a coordinate system
about
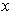 with
with
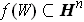 and
and
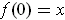 . Let
. Let
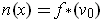 where
where
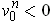 ,
,
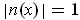 and
and
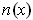 is perpendicular to
is perpendicular to
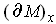 .
Note that
.
Note that
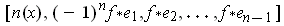 is the usual
orientation of
is the usual
orientation of
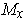 , and so, by definition,
, and so, by definition,
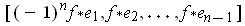 is the induced orientation on
is the induced orientation on
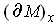 . But then
. But then
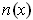 is the
unit normal in the second sense.
is the
unit normal in the second sense.
- If
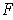 is a differentiable vector field on
is a differentiable vector field on
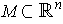 ,
show that there is an open set
,
show that there is an open set
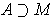 and a differentiable vector field
and a differentiable vector field
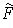 on
on
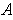 with
with
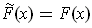 for
for
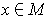 .
.
Let
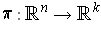 be the projection on the first
be the projection on the first
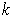 coordinates, where
coordinates, where
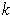 is the dimension of
is the dimension of
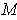 .
For every
.
For every
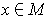 , there is a diffeomorphism
, there is a diffeomorphism
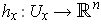 satisfying condition
satisfying condition
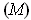 . For
. For
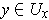 , define
, define
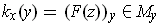 where
where
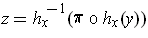 . Then
. Then
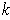 is a differentiable vector
field on
is a differentiable vector
field on
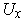 which extends the restriction of
which extends the restriction of
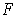 to
to
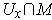 .
.
Let
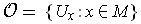 and
and
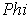 be a partition of unity
subordinate to
be a partition of unity
subordinate to
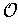 . For
. For
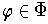 , choose a
, choose a
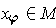 with
with
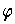 non-zero only for elements of
non-zero only for elements of
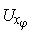 . Define
. Define
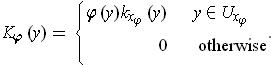
Finally, let
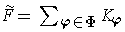 . Then
. Then
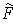 is a differentiable extension of
is a differentiable extension of
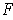 to
to
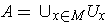 .
.
- If
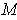 is closed, show that we can choose
is closed, show that we can choose
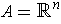 .
.
In the construction of part (a), one can assume that the
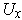 are open
rectangles with sides at most 1. Let
are open
rectangles with sides at most 1. Let
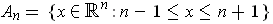 .
Since
.
Since
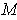 is closed,
is closed,
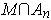 is compact, and so we can choose
a finite subcover of
is compact, and so we can choose
a finite subcover of
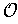 . We can then replace
. We can then replace
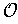 with the union of all these finite subcovers for all
with the union of all these finite subcovers for all
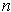 . This assures that
there are at most finitely many
. This assures that
there are at most finitely many
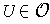 which intersect any given
bounded set. But now we see that the resulting
which intersect any given
bounded set. But now we see that the resulting
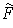 is a differentiable
extension of
is a differentiable
extension of
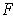 to all of
to all of
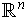 . In fact, we have now assured that
in a neighborhood of any point,
. In fact, we have now assured that
in a neighborhood of any point,
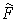 is a sum of finitely many
differentiable vector fields
is a sum of finitely many
differentiable vector fields
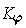 .
.
Note that the condition that
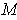 was needed as points
was needed as points
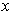 on the boundary of
the set
on the boundary of
the set
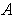 of part (a) could have infinitely many
of part (a) could have infinitely many
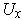 intersecting every
open neighborhood of
intersecting every
open neighborhood of
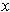 . For example, one might have a vector field
defined on
. For example, one might have a vector field
defined on
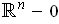 by
by
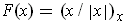 . This is a vector field
of outward pointing unit vectors, and clearly it cannot be extended to the
point
. This is a vector field
of outward pointing unit vectors, and clearly it cannot be extended to the
point
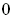 in a differentiable manner.
in a differentiable manner.
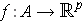 be as in Theorem 5-1.
be as in Theorem 5-1.
- If
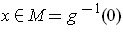 , let
, let
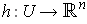 be
the essentially unique diffeomorphism such that
be
the essentially unique diffeomorphism such that
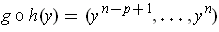 and
and
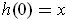 . Define
. Define
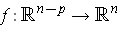 by
by
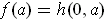 . Show that
. Show that
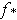 is 1-1 so that the
is 1-1 so that the
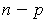 vectors
vectors
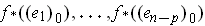 are linearly independent.
are linearly independent.
The notation will be changed. Let
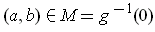 , and
, and
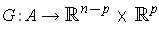 be defined, as in the proof
of the implicit function theorem, by
be defined, as in the proof
of the implicit function theorem, by
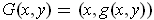 ; let
; let
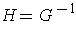 and
and
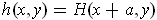 . Then
. Then
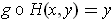 and so
and so
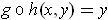 .
Also,
.
Also,
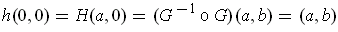 . Let
. Let
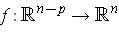 be defined by
be defined by
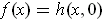 . We have changed the
order of the arguments to correct an apparent typographical error in the
problem statement.
. We have changed the
order of the arguments to correct an apparent typographical error in the
problem statement.
Now
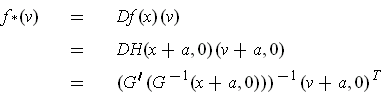
which is 1-1 because
 is a diffeomorphism. Since it is 1-1, it maps its
domain onto a space of dimension
is a diffeomorphism. Since it is 1-1, it maps its
domain onto a space of dimension
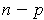 and so the vectors, being a basis,
must map to linearly independent vectors.
and so the vectors, being a basis,
must map to linearly independent vectors.
- Show that the orientations
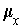 can be defined consistently,
so that
can be defined consistently,
so that
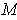 is orientable.
is orientable.
ince
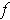 is a coordinate system about every point of
is a coordinate system about every point of
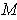 , this follows from
Problem 5-10 with
, this follows from
Problem 5-10 with
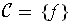 .
.
- If
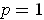 , show that the components of the outward normal at
, show that the components of the outward normal at
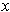 are some multiple of
are some multiple of
 .
.
We have
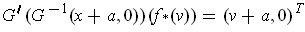 and so by considering the
components, we get
and so by considering the
components, we get
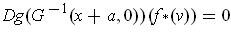 This shows that
This shows that
 is perpendicular to
is perpendicular to
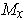 as desired.
as desired.
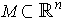 is an orientable
is an orientable
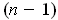 -dimensional
manifold, show that there is an open set
-dimensional
manifold, show that there is an open set
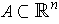 and a
differentiable
and a
differentiable
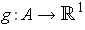 so that
so that
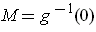 and
and
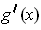 has rank 1 for
has rank 1 for
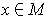 .
.
Choose an orientation
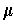 for
for
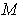 . As the hint says, Problem 5-4 does
the problem locally. Further, using Problem 5-13, we can assume locally
that the orientation imposed by
. As the hint says, Problem 5-4 does
the problem locally. Further, using Problem 5-13, we can assume locally
that the orientation imposed by
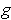 is the given orientation
is the given orientation
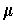 . By
replacing
. By
replacing
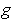 with its square, we can assume that
with its square, we can assume that
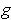 takes on non-negative
values. So for each
takes on non-negative
values. So for each
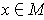 , we have a
, we have a
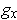 defined in an open neighborhood
defined in an open neighborhood
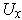 of
of
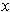 . Let
. Let
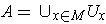 ,
,
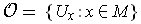 ,
and
,
and
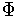 be a partion of unity subordinate to
be a partion of unity subordinate to
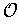 . Each
. Each
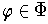 is non-zero only inside some
is non-zero only inside some
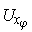 , and we can assume by
replacing the
, and we can assume by
replacing the
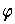 with sums of the
with sums of the
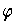 , that the
, that the
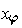 are distinct
for distinct
are distinct
for distinct
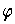 . Let
. Let
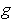 be defined by
be defined by
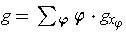 .
Then
.
Then
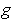 satisfies the desired conditions.
satisfies the desired conditions.
 be an
be an
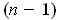 -dimensional manifold in
-dimensional manifold in
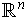 . Let
. Let
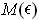 be the set of end-points of normal vectors (in both directions)
of length
be the set of end-points of normal vectors (in both directions)
of length
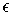 and suppose
and suppose
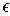 is small enough so that
is small enough so that
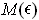 is also an
is also an
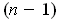 -dimensional manifold. Show that
-dimensional manifold. Show that
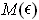 is orientable
(even if
is orientable
(even if
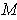 is not). What is
is not). What is
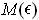 if
if
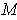 is the M"{o}bius strip?
is the M"{o}bius strip?
Let
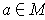 , and
, and
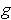 be as in Problem 5-4 in a neighborhood of
be as in Problem 5-4 in a neighborhood of
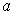 . Let
. Let
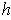 be as in Problem 5-13. Then we have a coordinate systems of
the form
be as in Problem 5-13. Then we have a coordinate systems of
the form
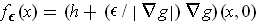 and
of the form
and
of the form
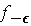 . Choose an orientation on each piece so
that adding
. Choose an orientation on each piece so
that adding
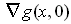 (respectively
(respectively
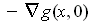 ) gives the usual
orientation on
) gives the usual
orientation on
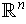 . This is an orientation for
. This is an orientation for
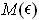 .
.
In the case of the M"{o}bius strip, the
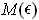 is equivalent to
a single ring
is equivalent to
a single ring
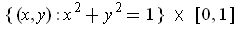 .
.
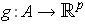 be as in Theorem 5-1. If
be as in Theorem 5-1. If
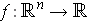 is differentiable and the maximum (or minimum) of
is differentiable and the maximum (or minimum) of
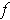 on
on
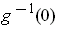 occurs at
occurs at
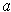 , show that there are
, show that there are
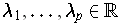 , such that
, such that
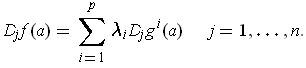
The maximum on
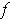 on
on
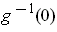 is sometimes called the maximum of
is sometimes called the maximum of
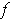 subject to the constraints
subject to the constraints
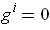 . One can attempt to
find
. One can attempt to
find
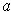 by solving the system of equations. In particular, if
by solving the system of equations. In particular, if
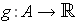 , we must solve
, we must solve
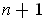 equations
equations
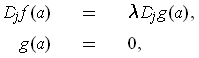
in
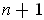 unknowns
unknowns
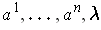 , which is often very simple
if we leave the equation
, which is often very simple
if we leave the equation
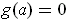 for last. This is Lagrange's
method, and the useful but irrelevant
for last. This is Lagrange's
method, and the useful but irrelevant
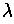 is called a Lagrangian
multiplier. The following problem gives a nice theoretical use for Lagrangian
multipliers.
is called a Lagrangian
multiplier. The following problem gives a nice theoretical use for Lagrangian
multipliers.
Let
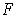 be a coordinate system in a neighborhood of the extremum at
be a coordinate system in a neighborhood of the extremum at
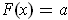 .
Then
.
Then
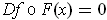 and so
and so
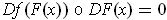 . Now the image of
. Now the image of
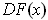 is just the tangent space
is just the tangent space
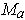 , and so the row of
, and so the row of
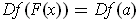 is perpendicular to the tangent space
is perpendicular to the tangent space
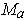 . But we also have
. But we also have
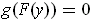 for all
for all
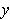 near
near
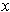 , and so
, and so
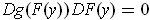 . In particular, this is
true at
. In particular, this is
true at
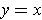 , and so the rows of
, and so the rows of
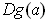 are also perpendicular to
are also perpendicular to
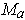 .
But,
.
But,
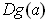 is of rank
is of rank
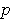 and
and
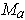 is of dimension
is of dimension
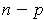 , and so the
rows of
, and so the
rows of
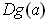 generate the entire subspace of vectors perpendicular to
generate the entire subspace of vectors perpendicular to
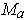 .
In particular,
.
In particular,
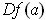 is in the subspace generated by the
is in the subspace generated by the
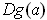 , which is
precisely the condition to be proved.
, which is
precisely the condition to be proved.
- Let
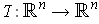 be self-adjoint with matrix
be self-adjoint with matrix
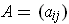 , so that
, so that
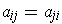 . If
. If
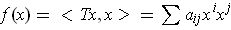 ,
show that
,
show that
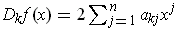 . By considering the maximum
of
. By considering the maximum
of
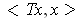 on
on
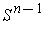 show that there is
show that there is
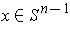 and
and
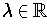 with
with
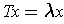 .
.
One has
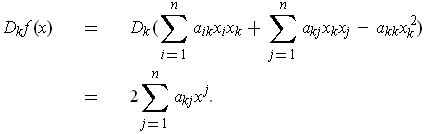
Apply Problem 5-16 with
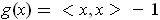 , so that the manifold is
, so that the manifold is
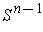 .
In this case,
.
In this case,
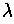 is a Lagrangian multiplier precisely when
is a Lagrangian multiplier precisely when
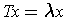 .
Since
.
Since
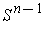 is compact,
is compact,
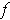 takes on a maximum on
takes on a maximum on
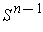 , and so
the maximum has a
, and so
the maximum has a
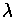 for which the Lagrangian multiplier equations
are true. This shows the result.
for which the Lagrangian multiplier equations
are true. This shows the result.
- If
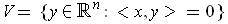 , show that
, show that
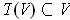 and
and
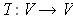 is self-adjoint.
is self-adjoint.
Suppose
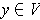 . Then
. Then
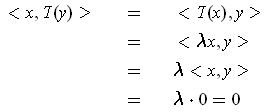
and so
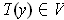 . This shows that
. This shows that
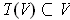 .
Since
.
Since
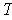 as a map of
as a map of
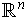 is self-adjoint and
is self-adjoint and
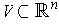 ,
it is clear that
,
it is clear that
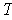 as a map of
as a map of
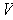 is also self-adjoint (cf p. 89 for the
definition).
is also self-adjoint (cf p. 89 for the
definition).
- Show that
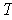 has a basis of eigenvectors.
has a basis of eigenvectors.
Proceed by induction on
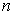 ; the case
; the case
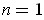 has already been shown.
Suppose It is true for dimension
has already been shown.
Suppose It is true for dimension
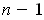 . Then apply part (a) to find
the eigenvector
. Then apply part (a) to find
the eigenvector
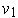 with eigenvalue
with eigenvalue
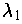 . Now,
. Now,
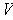 is of dimension
is of dimension
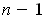 . So,
. So,
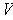 has a basis of eigenvectors
has a basis of eigenvectors
 with
eigenvalues
with
eigenvalues
 respectively. All the
respectively. All the
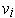 together is the basis of eigenvectors for
together is the basis of eigenvectors for
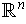 .
.