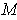 is an oriented one-dimensional manifold in
is an oriented one-dimensional manifold in
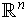 and
and
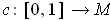 is orientation-preserving, show that
is orientation-preserving, show that
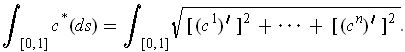
Consider the 1-form defined by
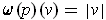 . This is the form which
matches the proposed solution since
. This is the form which
matches the proposed solution since
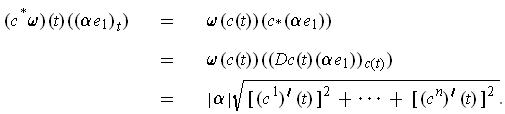
Furthermore, it is the volume element. To see this, choose an
orthonormal basis
 where
where
 where
where
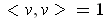 .
Then
.
Then
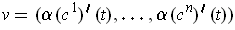 and
and
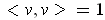 if and
only if
if and
only if
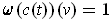 , as desired.
, as desired.
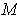 is an
is an
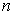 -dimensional manifold in
-dimensional manifold in
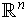 , with the
usual orientation, show that
, with the
usual orientation, show that
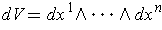 , so that
the volume of
, so that
the volume of
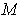 , as defined in this section, is the volume as defined
in Chapter 3. (Note that this depends on the numerical factor in the
definition of
, as defined in this section, is the volume as defined
in Chapter 3. (Note that this depends on the numerical factor in the
definition of
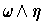 .)
.)
Let
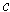 be an orientation-preserving
be an orientation-preserving
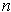 -cube, i.e.
-cube, i.e.
 . Let
. Let
 be an orthonormal basis with
the usual orientation.
By Theorem 4-9, we have
be an orthonormal basis with
the usual orientation.
By Theorem 4-9, we have
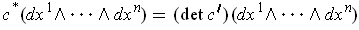 and so applying this to
and so applying this to
 gives
gives
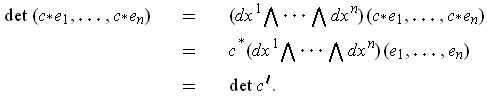
Since
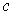 is
orientation preserving, it must be that
is
orientation preserving, it must be that
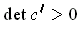 .
.
Now,
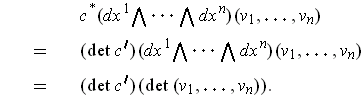
Now,
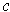 is orientation preserving, so
is orientation preserving, so
 must
have the usual orientation, i.e.
must
have the usual orientation, i.e.
 . But then
. But then
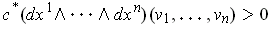 . Since this
is also equal to
. Since this
is also equal to
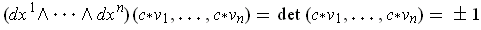 by orthonormality, it follows that
the value is precisely 1, and so it is the volume element in the sense of
this section.
by orthonormality, it follows that
the value is precisely 1, and so it is the volume element in the sense of
this section.
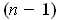 -dimensional
manifold in
-dimensional
manifold in
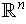 .
.
The generalization is
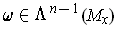 defined by
defined by
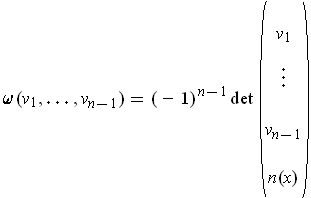
where
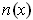 is the unit outward normal at
is the unit outward normal at
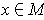 . As in the 2-dimensional
case,
. As in the 2-dimensional
case,
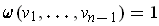 if the
if the
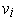 are an orthonormal basis
with orientation
are an orthonormal basis
with orientation
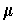 (where
(where
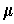 was the orientation used to determine
the outward normal). So
was the orientation used to determine
the outward normal). So
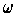 is the volume element
is the volume element
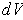 .
.
Expanding in terms of cofactors of the last row gives:
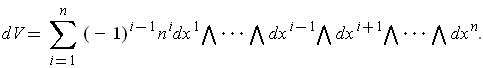
As in the 2-dimensional case,
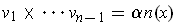 for
some scalar
for
some scalar
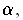 and so
and so
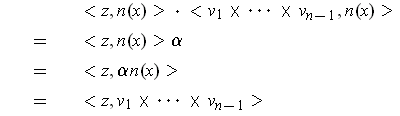
for all
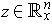 . Letting
. Letting
 , we get
, we get
- If
 is non-negative and the graph of
is non-negative and the graph of
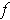 in the
in the
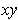 -plane is revolved around the
-plane is revolved around the
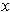 -axis in
-axis in
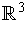 to
yield a surface
to
yield a surface
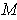 , show that the area of
, show that the area of
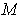 is
is
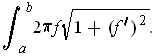
One can use singular 2-cubes of the form
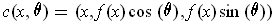 . The quantities
. The quantities
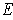 ,
,
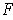 , and
, and
 calculate out to
calculate out to
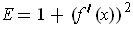 ,
,
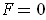 , and
, and
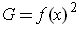 . So the surface area is
. So the surface area is
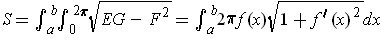 .
.
- Compute the area of
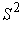 .
.
Apply part (a) with
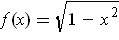 and
and
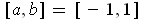 .
One has
.
One has
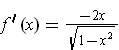 and
and
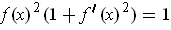 .
So
.
So
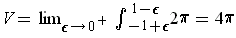 .
.
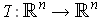 is a norm preserving linear
transformation and
is a norm preserving linear
transformation and
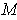 is a
is a
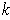 -dimensional manifold in
-dimensional manifold in
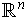 ,
show that
,
show that
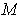 has the same volume as
has the same volume as
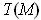 .
.
Although it is not stated, it is assumed that
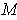 is orientable.
is orientable.
By Problem 1-7,
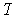 is inner product preserving and so it maps orthonormal
bases to orthonormal bases. Further, if
is inner product preserving and so it maps orthonormal
bases to orthonormal bases. Further, if
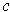 is a singular
is a singular
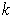 -cube which
is a coordinate system for
-cube which
is a coordinate system for
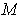 in a neighborhood of
in a neighborhood of
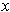 , then
, then
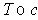 is a singular
is a singular
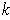 -cube which is a coordinate system for
-cube which is a coordinate system for
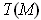 in a neighborhood
of
in a neighborhood
of
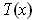 . Depending on the sign of
. Depending on the sign of
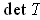 , the new
, the new
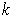 -cube is either
orientation preserving or reversing. In particular,
-cube is either
orientation preserving or reversing. In particular,
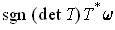 is the volume element of
is the volume element of
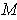 if
if
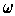 is the volume element of
is the volume element of
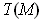 (which
is also orientable). Since the volume is just the integral of the volume
element and the integral is calculated via the
(which
is also orientable). Since the volume is just the integral of the volume
element and the integral is calculated via the
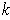 -cubes, it follows that
the volumes of
-cubes, it follows that
the volumes of
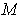 and
and
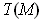 are equal.
are equal.
- If
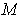 is a
is a
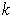 -dimensional manifold, show that an absolute
-dimensional manifold, show that an absolute
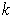 -tensor |dV| can be defined, even if
-tensor |dV| can be defined, even if
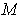 is not orientable, so that the
volume of
is not orientable, so that the
volume of
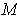 can be defined as
can be defined as
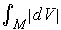 .
.
This was already done in Problem 5-21.
- If
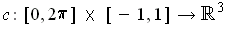 is defined
by
is defined
by
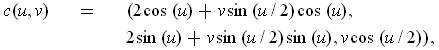
show that
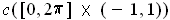 is a M@ouml;bius strip and find its area.
is a M@ouml;bius strip and find its area.
To see that it is a M@ouml;bius strip, note that in cylindrical coordinates, the equations are:
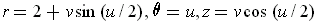 . In particular,
for fixed
. In particular,
for fixed
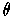 , we have
, we have
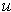 fixed and the path is a line segment
traversed from
fixed and the path is a line segment
traversed from
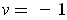 to
to
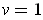 . Calculating the length of the line,
one gets that is a line segment of length 2. Again, for fixed
. Calculating the length of the line,
one gets that is a line segment of length 2. Again, for fixed
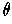 , the
line segment in the
, the
line segment in the
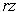 -plane has slope
-plane has slope
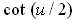 . Note that this varies
from
. Note that this varies
from
 down to
down to
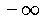 as
as
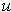 ranges from 0 to
ranges from 0 to
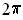 , i.e. the line
segment starts vertically at
, i.e. the line
segment starts vertically at
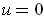 and reduces in slope until it becomes vertical
again at
and reduces in slope until it becomes vertical
again at
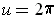 . This corresponds to twisting the paper 180 degrees as it
goes around the ring, which is the M@ouml;bius strip.
. This corresponds to twisting the paper 180 degrees as it
goes around the ring, which is the M@ouml;bius strip.
To find the area, one can actually, just use the formulas for an orientable surface, since one can just remove the line at
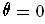 . In thatt
case one can verify, preferably with machine help, that
. In thatt
case one can verify, preferably with machine help, that
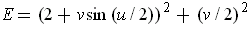 ,
,
 , and
, and
 . So the area is
. So the area is
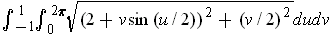 . Numerical
evaluation of the integral yields the approximation
. Numerical
evaluation of the integral yields the approximation
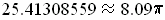 ,
which is just slightly larger than
,
which is just slightly larger than
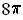 , the area of a circular ring of radius 2
and height 2.
, the area of a circular ring of radius 2
and height 2.
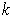 -form on a
-form on a
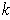 -dimensional manifold
-dimensional manifold
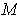 , show that
, show that
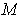 is orientable
is orientable
Suppose
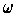 is the nowhere-zero
is the nowhere-zero
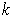 -form on
-form on
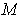 . If
. If
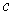 is a singular
is a singular
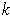 -cube, then for every
-cube, then for every
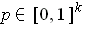 , we have
, we have
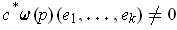 because the space
because the space
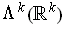 is of dimension 1. Choose
a
is of dimension 1. Choose
a
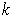 -cube so that the value is positive for some p. Then if it were negative
at another point
-cube so that the value is positive for some p. Then if it were negative
at another point
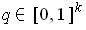 , then because this is a continuous function
from
, then because this is a continuous function
from
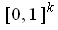 into
into
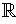 , the intermediate value theorem would guarantee
a point
, the intermediate value theorem would guarantee
a point
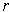 where the function were zero, which is absurd. So the value is
positive for all
where the function were zero, which is absurd. So the value is
positive for all
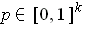 .
.
For every
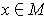 , choose a
, choose a
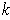 -cube of this type with
-cube of this type with
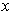 in its image.
Define
in its image.
Define
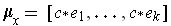 . This is well defined. Indeed,
if we had two such
. This is well defined. Indeed,
if we had two such
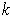 -cubes, say
-cubes, say
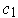 and
and
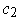 , then the
, then the
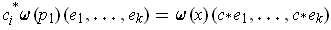 (where
(where
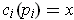 ) are positive for
) are positive for
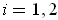 . But then the values are
of the same sign regardless of which non-zero k-form in
. But then the values are
of the same sign regardless of which non-zero k-form in
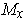 is used.
So, both maps define the same orientation on
is used.
So, both maps define the same orientation on
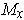 .
.
- If
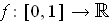 is differentiable and
is differentiable and
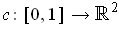 is defined by
is defined by
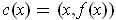 , show that
, show that
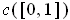 has length
has length
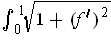 .
.
This is an immediate consequence of Problem 5-23.
- Show that this length is the least upper bound of lengths of
inscribed broken lines.
We will need
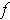 to be continuously differentiable, not just differentiable.
to be continuously differentiable, not just differentiable.
Following the hint, if
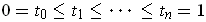 , then by the
mean value theorem,
, then by the
mean value theorem,
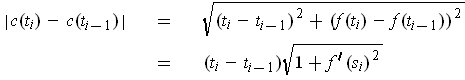
for some
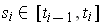 . Summing over
. Summing over
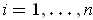 gives a Riemann sum
for
gives a Riemann sum
for
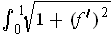 . Taking the limit as the mesh approaches 0,
shows that these approach the integral. Starting from any partition, and
taking successively finer partitions of the interval with the mesh approaching
zero, we get an increasing sequence of values with
limit the value of the integral; so the integral is the least upper bound of all
these lengths.
. Taking the limit as the mesh approaches 0,
shows that these approach the integral. Starting from any partition, and
taking successively finer partitions of the interval with the mesh approaching
zero, we get an increasing sequence of values with
limit the value of the integral; so the integral is the least upper bound of all
these lengths.
 defined on
defined on
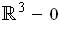 by
by
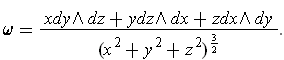
- Show that
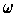 is closed.
is closed.
This is a straightforward calculation using the definition and Theorem 4-10. For example,
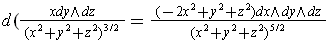 . The
other two terms give similar results, and the sum is zero.
. The
other two terms give similar results, and the sum is zero.
- Show that
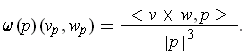
For
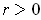 let
let
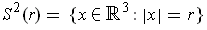 . Show that
. Show that
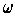 restricted to the tangent space of
restricted to the tangent space of
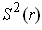 is
is
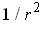 times the volume
element and that
times the volume
element and that
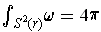 . Conclude that
. Conclude that
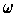 is not exact. Nevertheless, we denote
is not exact. Nevertheless, we denote
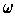 by
by
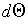 since, as we shall
see,
since, as we shall
see,
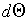 is the analogue of the 1-form
is the analogue of the 1-form
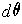 on
on
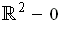 .
.
As in the proof of Theorem 5-6 (or Problem 5-25), the value of
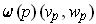 can be evaluated by expanding
can be evaluated by expanding
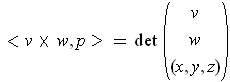 using cofactors
of the third row.
using cofactors
of the third row.
The second assertion follows from
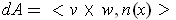 and the fact
that the outward directed normal can be taken to be
and the fact
that the outward directed normal can be taken to be
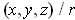 be
an appropriate choice of orientation. One has
be
an appropriate choice of orientation. One has
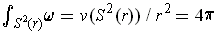 by Problem 5-26.
by Problem 5-26.
If
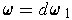 , then Stokes' Theorem would imply that
, then Stokes' Theorem would imply that
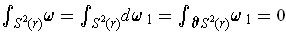 . Since the value is
. Since the value is
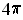 , we conclude that
, we conclude that
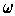 is not exact.
is not exact.
- If
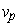 is a tangent vector such that
is a tangent vector such that
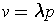 for some
for some
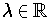 , show that
, show that
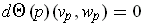 for all
for all
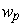 .
If a two-dimensional manifold
.
If a two-dimensional manifold
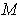 in
in
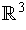 is part of a generalized
cone, that is,
is part of a generalized
cone, that is,
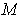 is the union of segments of rays through the origin, show
that
is the union of segments of rays through the origin, show
that
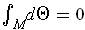 .
.
If
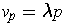 , then using part (b), one has
, then using part (b), one has
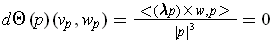 . By Problem 5-9, for any point
. By Problem 5-9, for any point
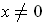 on the generalized cone, the line through
on the generalized cone, the line through
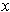 and the origin
lies on the surface and so its tangent line (the same line) is in
and the origin
lies on the surface and so its tangent line (the same line) is in
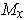 .
But then
.
But then
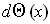 is identically 0 for all points
is identically 0 for all points
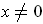 . But then
. But then
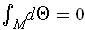 .
.
- Let
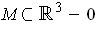 be a compact two-dimensionaal manifold-with-boundary
such that every ray through 0 intersects
be a compact two-dimensionaal manifold-with-boundary
such that every ray through 0 intersects
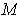 at most once (Figure 5-10).
The union of those rays through 0 which intersect
at most once (Figure 5-10).
The union of those rays through 0 which intersect
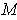 , is a solid cone
, is a solid cone
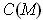 .
The solid angle subtended by
.
The solid angle subtended by
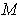 is defined as the area of
is defined as the area of
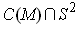 ,
or equivalently as
,
or equivalently as
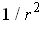 times the area of
times the area of
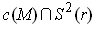 for
for
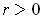 .
Prove that the solid angle subtended by
.
Prove that the solid angle subtended by
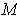 is
is
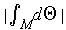 .
.
We take the orientations induced from the usual orientation of
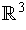 .
.
Following the hint, choose
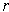 small enough so that there is a three
dimensional manifold-with-boundary N (as in Figure 5-10) such that
small enough so that there is a three
dimensional manifold-with-boundary N (as in Figure 5-10) such that
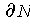 is the union of
is the union of
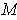 and
and
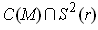 , and a part of a generalized
cone. (Actually,
, and a part of a generalized
cone. (Actually,
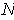 will be a manifold-with-corners; see the remarks at the
end of the next section.)
will be a manifold-with-corners; see the remarks at the
end of the next section.)
Note that this is essentially the same situation as in Problem 5-22. Applying Stokes' Theorem gives
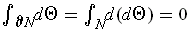 because
because
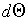 is closed by part (a). By part (c), the integral over the
part of the boundary making up part of a generalized cone is zero. The
orientation of the part of the boundary on
is closed by part (a). By part (c), the integral over the
part of the boundary making up part of a generalized cone is zero. The
orientation of the part of the boundary on
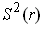 is opposite to that
of the orientation of the same set as a part of
is opposite to that
of the orientation of the same set as a part of
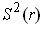 . So, we have
. So, we have
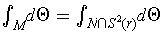 and the last integral is the
solid angle subtended by
and the last integral is the
solid angle subtended by
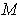 by the interpretation of
by the interpretation of
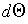 of part (b).
of part (b).
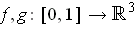 be nonintersecting closed
curves. Define the linking number l(f,g) of
be nonintersecting closed
curves. Define the linking number l(f,g) of
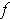 and
and
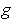 by (cf. Problem
4-34
by (cf. Problem
4-34
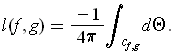
}
- Show that if (F,G) is a homotopy of nonintersecting closed
curves, then
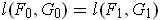 .
.
This follows immediately from Problem 4-34 (b) and Problem 5-31 (a).
- If
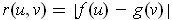 show that
show that
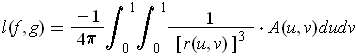
where
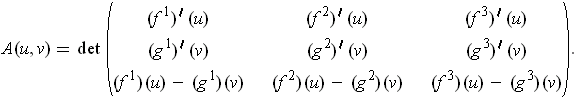
This follows by direct substitution using the expression for
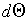 in the preamble to Problem 31.
in the preamble to Problem 31.
- Show that
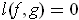 if
if
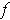 and
and
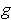 both lie in the
both lie in the
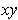 -plane.
-plane.
This follows from the formula in part (b) since the third column of the determinant defining
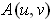 is zero.
is zero.
The curves of Figure 4-5(b) are given by
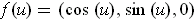 and
and
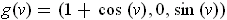 . You may easily convince yourself
that calculating
. You may easily convince yourself
that calculating
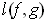 by the above integral is hopeless in this case.
The following problem shows how to find
by the above integral is hopeless in this case.
The following problem shows how to find
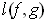 without explicit
calculations.
without explicit
calculations.
- If
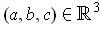 define
define
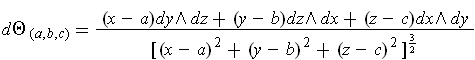
If
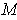 is a compact two-dimensional manifold-with-boundary in
is a compact two-dimensional manifold-with-boundary in
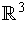 and
and
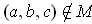 define
define
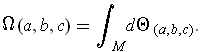
Let
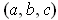 be a point on the same side of
be a point on the same side of
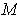 as the outward normal and
as the outward normal and
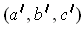 be a point on the opposite side. Show that by choosing
be a point on the opposite side. Show that by choosing
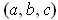 sufficiently close to
sufficiently close to
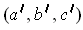 we can make
we can make
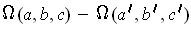 as close to
as close to
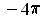 as desired.
as desired.
Following the hint, suppose that
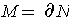 where
where
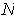 is a compact
manifold-with-boundary of dimension 3. Suppose
is a compact
manifold-with-boundary of dimension 3. Suppose
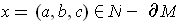 .
Removing a ball centered at
.
Removing a ball centered at
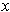 from the interior of
from the interior of
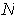 gives another
manifold-with-boundary
gives another
manifold-with-boundary
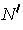 with boundary
with boundary
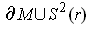 , where the
orientation on
, where the
orientation on
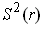 is opposite to that of the induced orientation.
So by Stokes' Theorem and Problem 5-31 (b),
is opposite to that of the induced orientation.
So by Stokes' Theorem and Problem 5-31 (b),
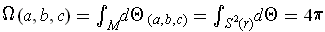 . (Note the
discrepancy in sign between this and the hint.) On the other
hand, if
. (Note the
discrepancy in sign between this and the hint.) On the other
hand, if
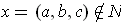 , then by Stokes' Theorem,
, then by Stokes' Theorem,
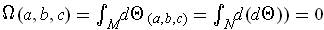 .
.
The rest of the proof will be valid only in the case where there is a 3-dimensional compact oriented manifold-with-boundary
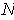 such that
such that
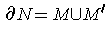 where
where
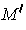 is a two-dimensional manifold. Then
is a two-dimensional manifold. Then
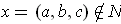 , and
and we can take
, and
and we can take
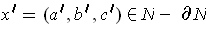 . So,
. So,
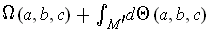 and
and
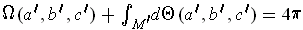 by the last paragraph. Subtracting gives
by the last paragraph. Subtracting gives
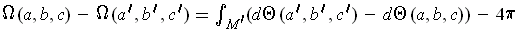 . The first term
can be made as small as we like by making
. The first term
can be made as small as we like by making
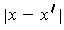 sufficiently small.
sufficiently small.
- Suppose
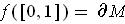 for some compact oriented
two-dimensional manifold-with-boundary
for some compact oriented
two-dimensional manifold-with-boundary
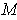 . (If
. (If
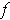 does not intersect
itself such an
does not intersect
itself such an
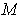 always exists, even if
always exists, even if
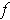 is knotted, see [6], page 138.)
Suppose that whenever
is knotted, see [6], page 138.)
Suppose that whenever
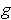 intersects
intersects
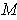 at
at
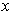 , the tangent vector
, the tangent vector
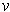 of
of
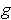 is not in
is not in
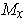 . Let
. Let
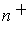 be the number of intersections where
be the number of intersections where
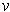 points in the same direction as the outward normal, and
points in the same direction as the outward normal, and
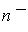 the
number of other intersections. If
the
number of other intersections. If
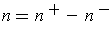 , show that
, show that
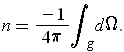
In the statement, what one means is that the component of
 in the outward
normal direction is either in the same or opposite direction as the outward
normal.
in the outward
normal direction is either in the same or opposite direction as the outward
normal.
Parameterize
 with
with
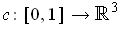 where
where
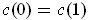 is not in
is not in
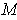 . Let
. Let
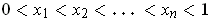 be the values where
be the values where
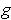 intersects
intersects
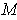 . To complete the proof, we will need to assume that
. To complete the proof, we will need to assume that
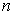 is finite. Let
is finite. Let
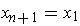 . Choose
. Choose
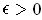 small enough
so that
small enough
so that
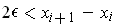 for all
for all
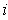 (where by
(where by
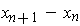 we mean
we mean
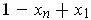 . One has
. One has
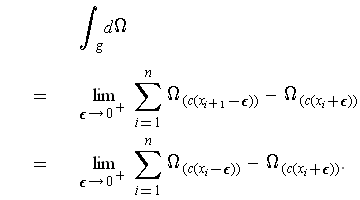
By part (a), if the tangent vector to
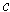 at
at
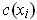 has a component in the
outward normal direction of
has a component in the
outward normal direction of
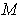 is positive, then
is positive, then
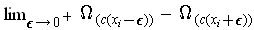 is
is
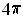 ; if it is negative, then it is
; if it is negative, then it is
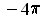 . So, the last paragraph has
. So, the last paragraph has
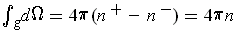 .
.
Note that this result differs from the problem statement by a sign.
- Prove that
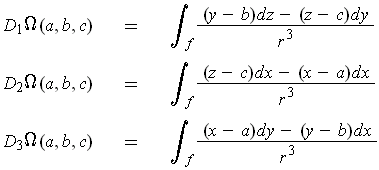
where
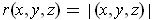 .
.
The definition of
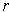 should be
should be
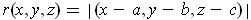 .
.
The proofs are analogous; we will show the first result. Start with
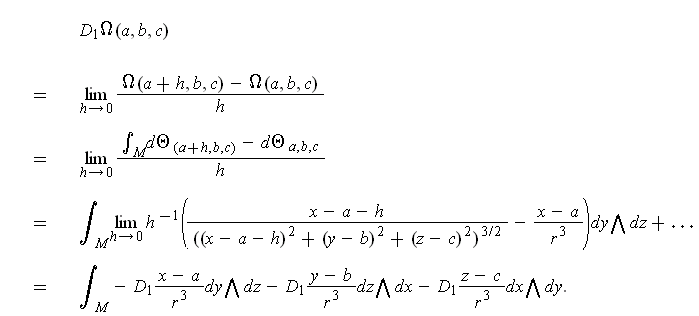
where we have used Problem 3-32 to interchange the order of the limit and the integral.
On the other hand, we have by Stokes' Theorem that
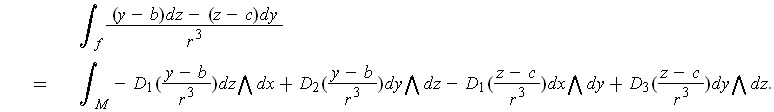
Comparing the two expressions, we see that two of the terms in the first expression match up with corresponding terms in the second expression. It remains to check that the remaining terms are equal. But a straightforward expansion gives:
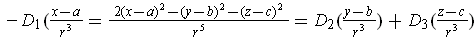 as desired.
as desired.
- Show that the integer
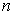 of (b) equals the integral of Problem
5-32(b), and use this result to show that
of (b) equals the integral of Problem
5-32(b), and use this result to show that
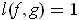 if
if
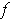 and
and
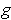 are the
curves of Figure 4-6 (b), while
are the
curves of Figure 4-6 (b), while
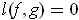 if
if
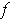 and
and
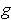 are the curves of
Figure 4-6 (c). (These results were known to Gauss [7]. The proofs outlined
here are from [4] pp. 409-411; see also [13], Volume 2, pp. 41-43.)
are the curves of
Figure 4-6 (c). (These results were known to Gauss [7]. The proofs outlined
here are from [4] pp. 409-411; see also [13], Volume 2, pp. 41-43.)
By part (c), one has
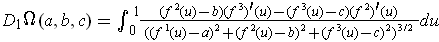 and so
and so
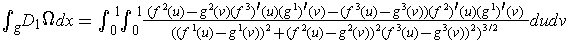 . Similar results hold for
. Similar results hold for
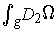 and
and
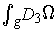 . One then substitutes into:
. One then substitutes into:
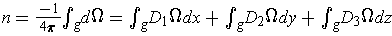 . After
collecting terms, we see that this is equal to the expression for
. After
collecting terms, we see that this is equal to the expression for
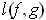 in Problem 5-32 (b). So,
in Problem 5-32 (b). So,
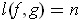 .
.
By inspection in Figure 4-6, one has
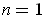 and
and
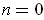 in parts
(b) and (c) of the figure. So, these are also the values of
in parts
(b) and (c) of the figure. So, these are also the values of
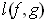 .
.