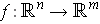 is differentiable
at
is differentiable
at
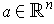 , then it is continuous at
, then it is continuous at
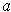 .
.
If
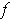 is differentiable at
is differentiable at
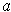 , then
, then
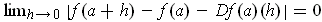 . So, we need only show that
. So, we need only show that
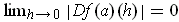 ,
but this follows immediately from Problem 1-10.
,
but this follows immediately from Problem 1-10.
 is said to be
independent of the second variable if for each
is said to be
independent of the second variable if for each
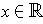 we have
we have
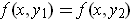 for all
for all
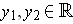 . Show that
. Show that
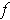 is independent
of the second variable if and only if there is a function
is independent
of the second variable if and only if there is a function
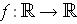 such that
such that
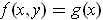 .
What is
.
What is
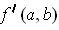 in terms of
in terms of
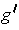 ?
?
The first assertion is trivial: If
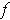 is independent of the second variable,
you can let
is independent of the second variable,
you can let
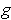 be defined by
be defined by
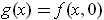 . Conversely, if
. Conversely, if
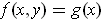 , then
, then
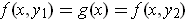 .
.
If
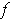 is independent of the second variable, then
is independent of the second variable, then
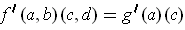 because:
because:
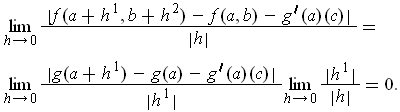
Note: Actually,
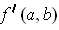 is the Jacobian, i.e. a 1 x 2 matrix. So,
it would be more proper to say that
is the Jacobian, i.e. a 1 x 2 matrix. So,
it would be more proper to say that
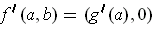 , but I will often
confound
, but I will often
confound
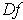 with
with
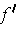 , even though one is a linear transformation
and the other is a matrix.
, even though one is a linear transformation
and the other is a matrix.
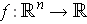 is independent
of the first variable and find
is independent
of the first variable and find
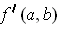 for such
for such
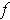 . Which functions are
independent of the first variable and also of the second variable?
. Which functions are
independent of the first variable and also of the second variable?
The function
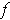 is independent of the first variable if and only if
is independent of the first variable if and only if
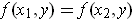 for all
for all
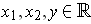 . Just as before,
this is equivalent to their being a function
. Just as before,
this is equivalent to their being a function
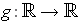 such that
such that
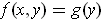 for all
for all
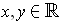 . An argument similar
to that of the previous problem shows that
. An argument similar
to that of the previous problem shows that
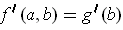 .
.
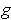 be a continuous real-valued function on the unit circle
be a continuous real-valued function on the unit circle
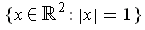 such that
such that
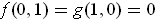 and
and
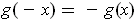 . define
. define
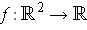 by
by
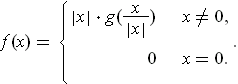
- If
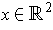 and
and
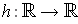 is defined
by
is defined
by
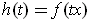 , show that
, show that
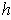 is differentiable.
is differentiable.
One has
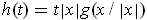 when
when
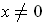 and
and
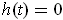 otherwise. In
both cases,
otherwise. In
both cases,
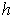 is linear and hence differentiable.
is linear and hence differentiable.
- Show that
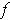 is not differentiable at (0, 0) unless
is not differentiable at (0, 0) unless
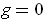 .
.
Suppose
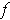 is differentiable at
is differentiable at
 with, say,
with, say,
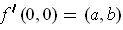 .
Then one must have:
.
Then one must have:
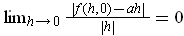 .
But
.
But
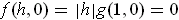 and so
and so
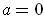 . Similarly, one gets
. Similarly, one gets
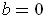 .
More generally, using the definition of derivative, we get for fixed
.
More generally, using the definition of derivative, we get for fixed
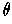 :
:
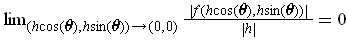 . But
. But
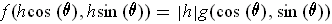 , and so we see that this just says that
, and so we see that this just says that
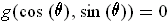 for all
for all
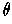 . Thus
. Thus
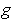 is identically zero.
is identically zero.
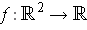 be defined by
be defined by
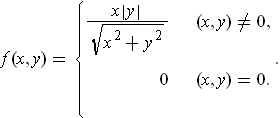
Show that
 is a function of the kind considered in Problem 2-4, so that
is a function of the kind considered in Problem 2-4, so that
 is not differentiable at
is not differentiable at
 .
.
Define
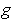 by
by
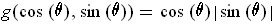 for all
for all
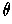 . Then it is trivial to show that
. Then it is trivial to show that
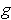 satisfies all the
properties of Problem 2-4 and that the function
satisfies all the
properties of Problem 2-4 and that the function
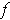 obtained from this
obtained from this
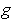 is as in the statement of this problem.
is as in the statement of this problem.
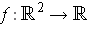 be defined by
be defined by
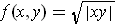 . Show that
. Show that
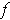 is not differentiable at 0.
is not differentiable at 0.
Just as in the proof of Problem 2-4, one can show that, if
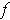 were
differentiable at 0, then
were
differentiable at 0, then
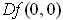 would be the zero map. On the other hand,
by approaching zero along the 45 degree line in the first quadrant, one
would then have:
would be the zero map. On the other hand,
by approaching zero along the 45 degree line in the first quadrant, one
would then have:
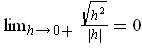 in spite
of the fact that the limit is clearly 1.
in spite
of the fact that the limit is clearly 1.
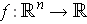 be a function such that
be a function such that
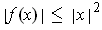 . Show that
. Show that
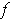 is differentiable at 0.
is differentiable at 0.
In fact,
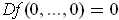 by the squeeze principle using
by the squeeze principle using
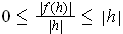 .
.
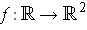 . Prove that
. Prove that
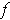 is
differentiable at
is
differentiable at
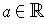 if and only if
if and only if
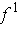 and
and
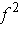 are, and in
this case
are, and in
this case
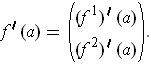
Suppose that
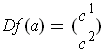 . Then one
has the inequality:
. Then one
has the inequality:
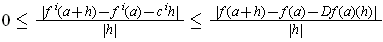 . So, by the squeeze principle,
. So, by the squeeze principle,
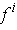 must be differentiable at
must be differentiable at
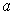 with
with
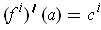 .
.
On the other hand, if the
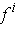 are differentiable at
are differentiable at
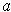 , then use the
inequality derived from Problem 1-1:
, then use the
inequality derived from Problem 1-1:
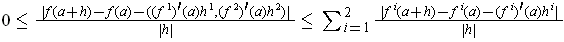 and the squeeze principle to conclude that
and the squeeze principle to conclude that
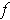 is differentiable at
is differentiable at
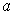 with the desired derivative.
with the desired derivative.
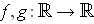 are equal up
to
are equal up
to
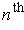 order at
order at
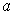 if
if
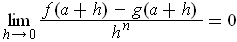
- Show that
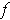 is differentiable at
is differentiable at
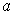 if and only if there is
a function
if and only if there is
a function
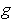 of the form
of the form
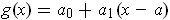 such that
such that
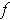 and
and
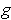 are equal up to first order at
are equal up to first order at
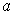 .
.
If
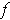 is differentiable at
is differentiable at
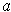 , then the function
, then the function
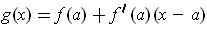 works by the definition of derivative.
works by the definition of derivative.
The converse is not true. Indeed, you can change the value of
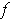 at
at
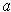 without changing whether or not
without changing whether or not
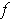 and
and
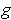 are equal up to first order. But
clearly changing the value of
are equal up to first order. But
clearly changing the value of
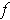 at
at
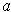 changes whether or not
changes whether or not
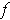 is
differentiable at
is
differentiable at
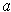 .
.
To make the converse true, add the assumption that
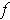 be continuous at
be continuous at
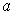 :
If there is a
:
If there is a
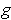 of the
specified form with
of the
specified form with
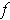 and
and
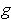 equal up to first order, then
equal up to first order, then
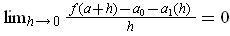 . Multiplying
this by
. Multiplying
this by
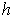 , we see that
, we see that
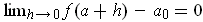 . Since
. Since
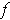 is continuous, this means that
is continuous, this means that
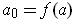 . But then the condition
is equivalent to the assertion that
. But then the condition
is equivalent to the assertion that
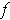 is differentiable at
is differentiable at
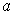 with
with
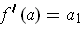 .
.
- If
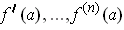 exist, show that
exist, show that
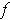 and the function
and the function
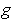 defined by
defined by
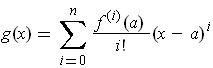
are equal up to
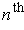 order at a.
order at a.
Apply L'Hôpital's Rule n - 1 times to the limit
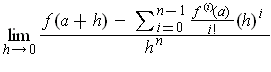
to see that the value of the limit is
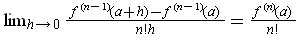 . On the other hand, one has:
. On the other hand, one has:
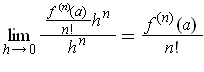
Subtracting these two results gives shows that
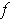 and
and
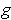 are equal up to
are equal up to
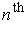 order at
order at
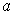 .
.