Exercises: Chapter 2, Section 3
-
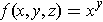
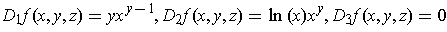 .
.
-
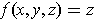
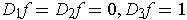 .
.
-
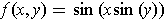
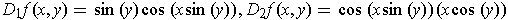 .
.
-
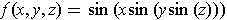
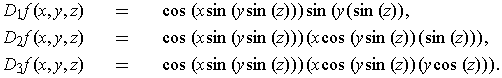
-
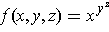
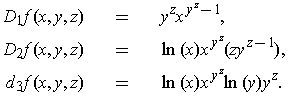
-
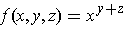
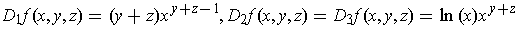 .
.
-
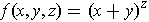
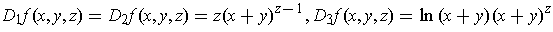 .
.
-
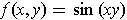
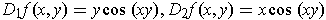 .
.
-
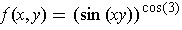
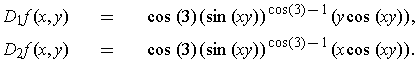
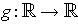 is continuous):
is continuous):
-
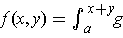
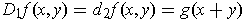 .
.
-
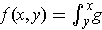
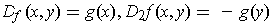 .
.
-
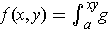
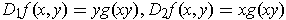 .
.
-
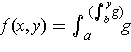
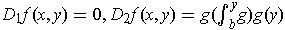 .
.

find
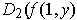 .
.
Since
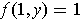 , one has
, one has
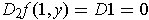 .
.
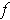 in terms of the derivatives
of
in terms of the derivatives
of
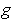 and
and
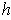 if
if
-
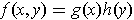
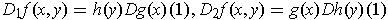 .
.
-
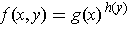
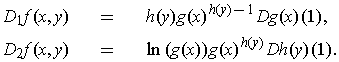
-
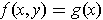
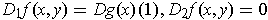 .
.
-
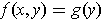
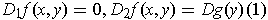 .
.
-
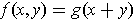
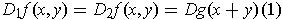 .
.
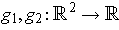 be continuous. Define
be continuous. Define
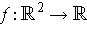 by
by
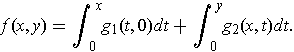
- Show that
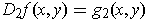
True since the first term depends only on
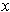 .
.
- How should
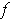 be defined so that
be defined so that
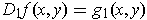 ?
?
One could let
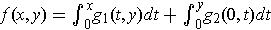 .
.
- Find a function
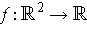 such that
such that
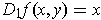 and
and
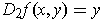 .
.
One could let
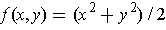 .
.
Find one such that
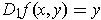 and
and
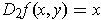 .
.
One could let
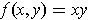 .
.
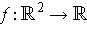 and
and
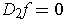 , show that
, show that
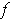 is independent of the second variable. If
is independent of the second variable. If
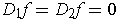 , show that
, show that
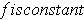 .
.
By the mean value theorem, one knows that if a function of one variable
has zero derivative on a closed interval
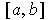 , then it is constant on
that interval. Both assertions are immediate consequences of this result.
, then it is constant on
that interval. Both assertions are immediate consequences of this result.
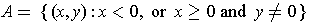 .
.
- If
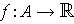 and
and
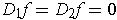 , show that
, show that
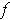 is a constant.
is a constant.
Suppose
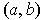 and
and
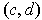 are arbitrary points of
are arbitrary points of
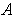 . Then the
line segment from
. Then the
line segment from
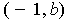 to
to
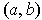 , from
, from
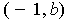 to
to
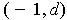 , and
from
, and
from
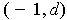 to
to
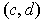 are all contained in
are all contained in
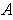 . By the proof of Problem
2-22, it follows that
. By the proof of Problem
2-22, it follows that
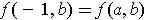 ,
,
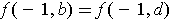 , and
, and
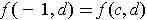 . So
. So
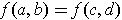 .
.
- Find a function
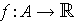 such that
such that
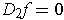 but
but
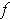 is not independent of the second variable.
is not independent of the second variable.
One could let
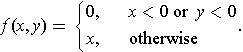 .
.
 by
by
- Show that
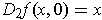 for all
for all
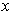 and
and
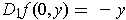 for
all
for
all
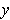 .
.
One has
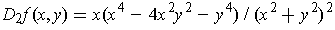 when
when
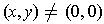 ,
and
,
and
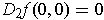 since
since
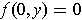 . Further, one has
. Further, one has
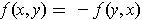 and so
and so
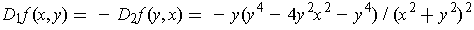 for all
for all
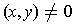 and
and
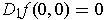 (because
(because
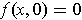 ). The
assertions follow immediately by substituting
). The
assertions follow immediately by substituting
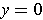 into one formula
and
into one formula
and
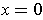 in the other.
in the other.
- Show that
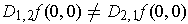 .
.
Using part (a), one has
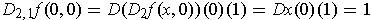 and
and
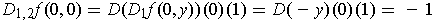 .
.
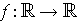 by
by
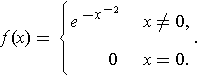
-
Show that
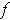 is a
is a
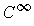 function, and
function, and
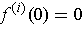 for all
for all
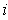 .
.
Consider the function
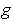 defined by
defined by
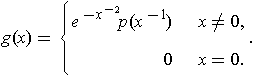
where
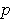 is a polynomial.
Then, one has
is a polynomial.
Then, one has
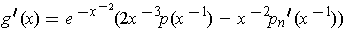 for
for
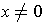 . By induction on
. By induction on
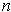 , define
, define
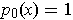 and
and
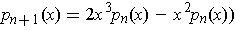 . Then it follows that
. Then it follows that
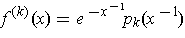 for all
for all
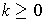 . In particular, function
. In particular, function
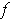 is
is
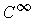 for all
for all
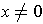 .
.
Now, suppose by induction on
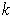 , that
, that
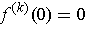 . We have
. We have
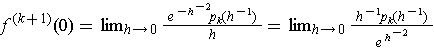 . To show that
this limit is zero, it suffices to show that
. To show that
this limit is zero, it suffices to show that
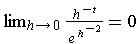 for each integer
for each integer
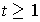 . But this is
an easy induction using L'Hôpital's rule:
. But this is
an easy induction using L'Hôpital's rule:
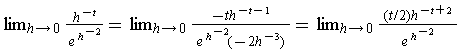 .
.
- Let
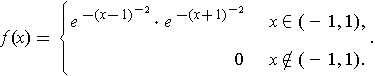
- Show that
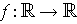 is a
is a
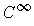 function which is positive on (-1, 1) and 0 elsewhere.
function which is positive on (-1, 1) and 0 elsewhere.
For points other than 1 and -1, the result is obvious. At each of the exceptional points, consider the derivative from the left and from the right, using Problem 2-25 on the side closest to the origin.
- Show that there is a
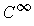 function
function
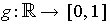 such that
such that
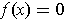 for
for
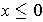 and
and
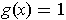 for
for
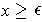 .
.
Following the hint, let
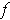 be as in Problem 2-25 and
be as in Problem 2-25 and
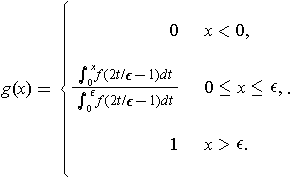 Now use Problem 2-25 to prove that
Now use Problem 2-25 to prove that
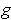 works.
works.
- If
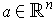 , define
, define
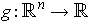 by
by
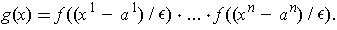
Show that
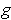 is a
is a
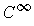 function which is positive on
function which is positive on

and zero elsewhere.
This follows from part (a).
- If
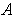 is open and
is open and
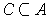 is compact, show that there is a
non-negative
is compact, show that there is a
non-negative
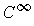 function
function
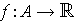 such that
such that
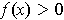 for
for
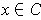 and
and
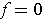 outside of some closed set contained in
outside of some closed set contained in
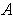 .
.
Let
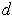 be the distance between
be the distance between
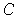 and the complement of
and the complement of
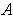 , and choose
, and choose
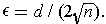 For each
For each
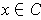 , let
, let
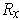 be the open rectangle
centered at
be the open rectangle
centered at
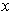 with sides of length
with sides of length
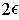 . Let
. Let
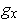 be the function
defined for this rectangle as in part (c). Since the set of these rectangles
is an open cover of the compact set
be the function
defined for this rectangle as in part (c). Since the set of these rectangles
is an open cover of the compact set
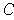 , a finite number of them also cover
, a finite number of them also cover
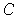 ;
say the rectangles corresponding to
;
say the rectangles corresponding to
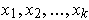 form a subcover.
Finally, let
form a subcover.
Finally, let
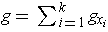 .
.
Since we have a subcover of
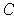 , we have
, we have
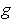 positive on
positive on
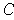 . The choice of
. The choice of
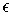 guarantees that the union of the closures of the rectangles in
the subcover is contained in
guarantees that the union of the closures of the rectangles in
the subcover is contained in
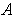 and
and
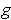 is clearly zero outside of this
union. This proves the assertion.
is clearly zero outside of this
union. This proves the assertion.
- Show that we can choose such an
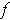 so that
so that
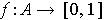 and
and
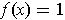 for
for
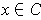 .
.
Let
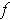 be as in part (d). We know that
be as in part (d). We know that
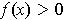 for all
for all
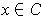 . Since
. Since
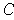 is compact, one knows that
is compact, one knows that
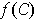 is attains its minimum
is attains its minimum
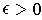 (Problem 1-29). As suggested in the hint, replace
(Problem 1-29). As suggested in the hint, replace
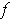 with
with
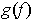 where
where
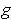 is the function of part (b). It is easy to verify that this new
is the function of part (b). It is easy to verify that this new
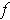 satisfies the required conditions.
satisfies the required conditions.
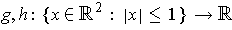 by
by
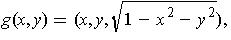
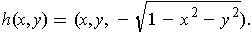
Show that the maximum of
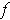 on
on
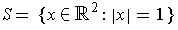 is either
the maximum of
is either
the maximum of
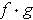 or the maximum of
or the maximum of
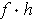 on
on
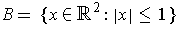 .
.
This is obvious because
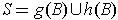 .
.