-
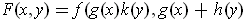
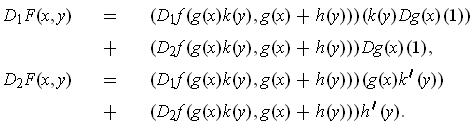
-
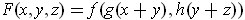
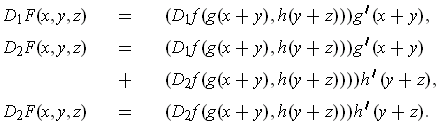
-
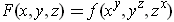
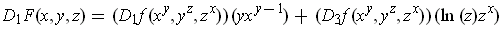 ,
,
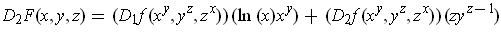 ,
,
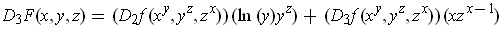 .
.
-
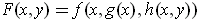
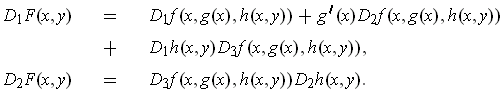
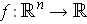 . For
. For
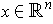 , the
limit
, the
limit
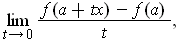
if it exists, is denoted
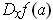 and called the directional derivative
of
and called the directional derivative
of
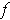 at
at
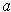 , in the direction
, in the direction
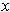 .
.
- Show that
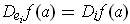 .
.
This is obvious from the definitions.
- Show that
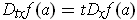 .
.
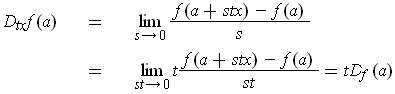
- If
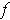 is differentiable at
is differentiable at
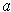 , show that
, show that
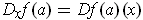 and therefore
and therefore
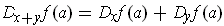 .
.
One has
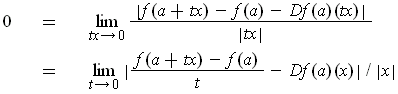
which shows the result whenever
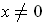 . The case when
. The case when
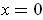 is trivially true.
is trivially true.
The last assertion follows from the additivity of the function
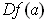 .
.
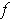 be defined as in Problem 2-4. Show that
be defined as in Problem 2-4. Show that
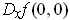 exists for all
exists for all
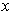 , but if
, but if
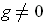 , then
, then
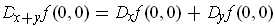 is not true for all
is not true for all
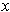 and all
and all
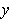 .
.
With the notation of Problem 2-4, part (a) of that problem says that
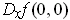 exists for all
exists for all
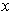 . Now suppose
. Now suppose
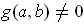 . Then
. Then
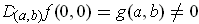 , But
, But
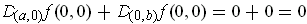 .
.
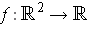 be defined as in Problem 1-26.
Show that
be defined as in Problem 1-26.
Show that
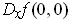 exists for all
exists for all
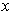 , although
, although
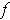 is not even continuous
at (0,0).
is not even continuous
at (0,0).
By Problem 1-26 (a),
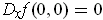 for all
for all
 .
.
- Let
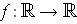 be defined by
be defined by
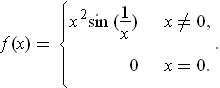
Show that
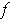 is differentiable at 0 but
is differentiable at 0 but
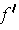 is not continuous at 0.
is not continuous at 0.
Clearly,
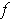 is differentiable at
is differentiable at
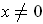 . At
. At
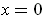 , one
has
, one
has
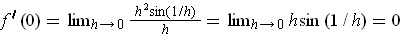 since
since
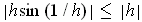 .
.
For
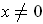 , one has
, one has
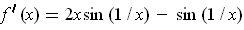 . The first term has
limit 0 as
. The first term has
limit 0 as
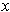 approaches 0. But the second term takes on all values between
-1 and 1 in every open neighborhood of
approaches 0. But the second term takes on all values between
-1 and 1 in every open neighborhood of
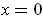 . So,
. So,
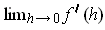 does not even exist.
does not even exist.
- Let
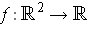 be defined by
be defined by
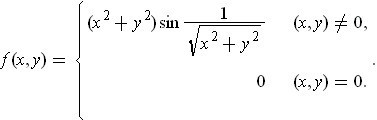
Show that
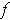 is differentiable at (0,0) but that
is differentiable at (0,0) but that
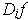 is not continuous
at
is not continuous
at
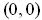 .
.
The derivative at (0, 0) is the zero linear transformation because
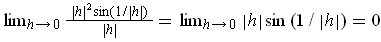 , just as in part (a).
, just as in part (a).
However,
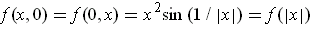 for
for
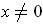 where
where
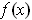 is as in part (a). It follows from the differentiability of
is as in part (a). It follows from the differentiability of
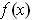 ,
that
,
that
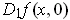 and
and
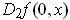 are defined for
are defined for
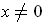 . (The argument
given above also shows that they are defined and 0 at
. (The argument
given above also shows that they are defined and 0 at
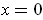 .) Further
the partials are equal to
.) Further
the partials are equal to
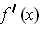 up to a sign, and so they cannot be
continuous at 0.
up to a sign, and so they cannot be
continuous at 0.
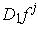 at
at
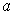 may be eliminated from
the hypothesis of Theorem 2-8.
may be eliminated from
the hypothesis of Theorem 2-8.
Proceed as in the proof of Theorem 2-8 for all
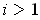 . In the
. In the
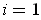 case,
it suffices to note that
case,
it suffices to note that
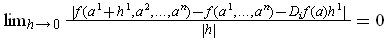 follows from the definition of
follows from the definition of
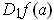 . This is all that is needed in
the rest of the proof.
. This is all that is needed in
the rest of the proof.
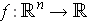 is homogeneous
of degree
is homogeneous
of degree
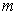 if
if
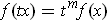 for all
for all
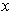 and
and
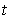 . If
. If
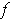 is also
differentiable, show that
is also
differentiable, show that
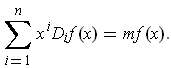
Applying Theorem 2-9 to
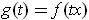 gives
gives
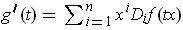 .
On the other hand,
.
On the other hand,
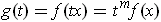 and so
and so
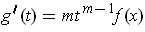 .
Substituting
.
Substituting
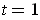 in these two formulas show the result.
in these two formulas show the result.
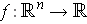 is differentiable and
is differentiable and
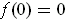 ,
prove that there exist
,
prove that there exist
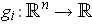 such that
such that
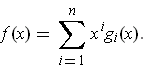
Following the hint, let
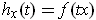 . Then
. Then
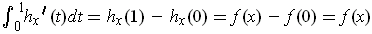 . On the other hand, Theorem 2-9 gives
. On the other hand, Theorem 2-9 gives
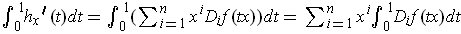 . So, we have the result with
. So, we have the result with
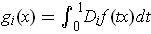 .
.