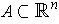 be an open set and
be an open set and
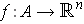 a continusously differentiable 1-1 function such that
a continusously differentiable 1-1 function such that
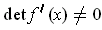 for all
for all
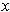 . Show that
. Show that
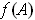 is an open set and
is an open set and
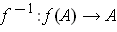 is differentiable. Show also that
is differentiable. Show also that
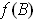 is open for any open set
is open for any open set
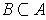 .
.
For every
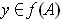 , there is an
, there is an
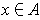 with
with
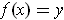 . By Theorem 2-11,
there is an open set
. By Theorem 2-11,
there is an open set
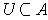 and an open subset
and an open subset
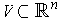 such that
such that
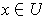 and
and
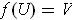 . Since clearly
. Since clearly
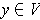 , this shows that
, this shows that
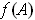 is open. Furthermore
is open. Furthermore
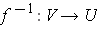 is differentiable.
It follows that
is differentiable.
It follows that
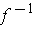 is differentiable at
is differentiable at
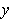 . Since
. Since
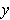 was arbitrary,
it follows that
was arbitrary,
it follows that
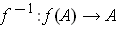 is differentiable.
is differentiable.
By applying the previous results to the set
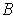 in place of
in place of
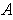 , we see that
, we see that
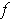 is open.
is open.
- Let
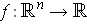 be a continuously differentiable
function. Show that
be a continuously differentiable
function. Show that
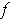 is not 1-1.
is not 1-1.
We will show the result is true even if
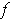 is only defined in a non-empty open
subset of
is only defined in a non-empty open
subset of
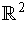 .
Following the hint, we know that
.
Following the hint, we know that
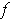 is not constant in any open set. So,
suppose we have
is not constant in any open set. So,
suppose we have
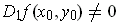 (the case where
(the case where
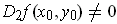 is analogous). Then there is an open neighborhood
is analogous). Then there is an open neighborhood
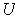 of
of
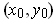 with
with
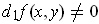 for all
for all
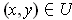 . The function
. The function
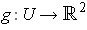 defined by
defined by
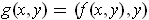 satisfies
satisfies
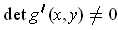 for all
for all
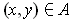 . Assuming that
. Assuming that
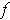 and hence
and hence
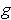 are 1-1, we can apply Problem
2-36. The inverse function is clearly of the form
are 1-1, we can apply Problem
2-36. The inverse function is clearly of the form
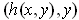 and so
and so
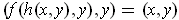 for all
for all
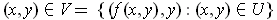 .
Now
.
Now
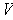 is open but each horizontal line intersects
is open but each horizontal line intersects
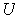 at most once
since
at most once
since
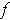 is 1-1. This is a contradiction since
is 1-1. This is a contradiction since
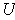 is non-empty and open.
is non-empty and open.
- Generalize this result to tthe case of a continuously differentiable
function
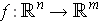 with
with
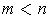 .
.
By replacing
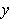 with a vector of variables, the proof of part (a) generalizes
to the case where
with a vector of variables, the proof of part (a) generalizes
to the case where
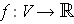 is a function defined on an
open subset
is a function defined on an
open subset
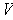 of
of
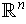 where
where
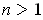 .
.
For the general case of a map
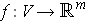 where
where
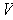 is
an open subset of
is
an open subset of
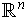 with
with
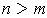 , if
, if
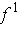 is constant in a non-empty
open set
is constant in a non-empty
open set
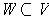 , then we replace
, then we replace
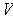 with
with
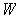 and drop out
and drop out
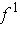 reducing the value of
reducing the value of
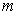 by one. On the other hand, if
by one. On the other hand, if
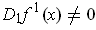 for some
for some
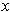 , then consider the function
, then consider the function
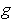 defined by
defined by
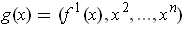 . Just as in part (a), this will be invertible on
an open subset of
. Just as in part (a), this will be invertible on
an open subset of
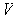 and its inverse will look like
and its inverse will look like
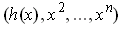 .
Replace
.
Replace
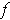 with
with
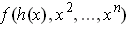 . Note that we have made
. Note that we have made
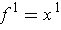 . Again, by restricting to an appropriate rectangle, we can
simply fix the value of
. Again, by restricting to an appropriate rectangle, we can
simply fix the value of
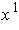 and get a 1-1 function defined on on a rectangle
in one less dimension and mapping into a space of dimension one less.
By repeating this process, one eventually gets to the case where
and get a 1-1 function defined on on a rectangle
in one less dimension and mapping into a space of dimension one less.
By repeating this process, one eventually gets to the case where
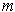 is
equal to 1, which we have already taken care of.
is
equal to 1, which we have already taken care of.
- If
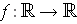 satisfies
satisfies
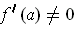 for all
for all
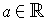 , show that
, show that
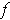 is 1-1 on all of
is 1-1 on all of
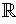 .
.
Suppose one has
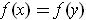 for some
for some
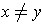 . By the mean value theorem,
there is a
. By the mean value theorem,
there is a
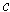 between
between
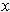 and
and
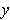 such that
such that
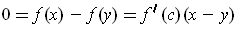 .
Since both factors on the right are non-zero, this is impossible.
.
Since both factors on the right are non-zero, this is impossible.
- Define
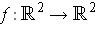 by
by
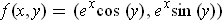 . Show that
. Show that
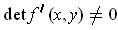 for all
for all
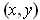 but
but
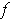 is not 1-1.
is not 1-1.
Clearly,
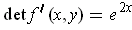 for all
for all
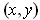 . The function is not 1-1 since
. The function is not 1-1 since
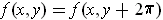 for all
for all
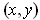 .
.
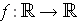 defined by
defined by
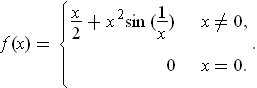
to show that continuity of the derivative cannot be eliminated from the hypothesis of Theorem 2-11.
Clearly,
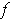 is differentiable for
is differentiable for
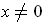 . At
. At
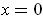 , one has
, one has
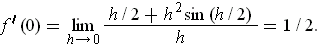
So
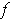 satisfies the conditions of Theorem 2-11 at
satisfies the conditions of Theorem 2-11 at
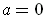 except that it
is not continuously differentiable at 0 since
except that it
is not continuously differentiable at 0 since
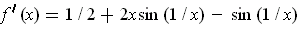 for
for
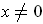 .
.
Now
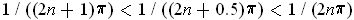 and it is straightforward
to verify that
and it is straightforward
to verify that
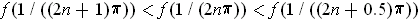 for
all sufficiently large positive integers
for
all sufficiently large positive integers
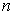 . By the intermediate value
theorem, there is a
. By the intermediate value
theorem, there is a
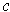 between
between
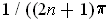 and
and
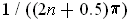 where
where
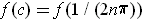 . By taking n larger and larger, we see that
. By taking n larger and larger, we see that
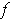 is not 1-1 on any neighborhood of 0.
is not 1-1 on any neighborhood of 0.