Define
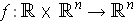 by
by
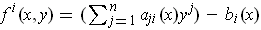 for
for
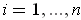 .
One has
.
One has
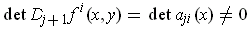 for all
for all
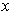 . The
determinant condition guarantees that for each
. The
determinant condition guarantees that for each
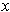 , there is exactly
one solution of
, there is exactly
one solution of
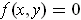 , call that solution
, call that solution
 .
.
Now, for each
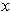 , the Implicit function theorem says that there is
a function
, the Implicit function theorem says that there is
a function
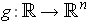 defined in an open neighborhood
of
defined in an open neighborhood
of
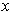 and such that
and such that
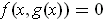 and
and
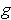 is differentiable. By the
uniqueness of the solutions in the last paragraph, it must be that
is differentiable. By the
uniqueness of the solutions in the last paragraph, it must be that
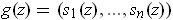 for all
for all
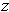 in the domain of
in the domain of
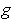 . In
particular, the various functions
. In
particular, the various functions
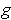 all glue together into a single
function defined on all of
all glue together into a single
function defined on all of
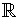 and differentiable everywhere.
and differentiable everywhere.
By differentiating the relation
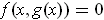 , one gets
, one gets
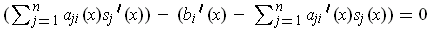 for
for
 . Note that this is of the same form as the set of
equations for
. Note that this is of the same form as the set of
equations for
 except that the right hand side functions
have changed. An explicit formula can be obtained by using Cramer's
rule.
except that the right hand side functions
have changed. An explicit formula can be obtained by using Cramer's
rule.
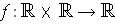 be differentiable.
For each
be differentiable.
For each
 defined
defined
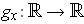 by
by
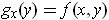 . Suppose that for each
. Suppose that for each
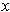 there is a unique
there is a unique
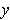 with
with
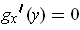 ; let
; let
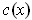 be this
be this
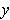 .
.
In this problem, it is assumed that
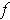 was meant to be continuously differentiable.
was meant to be continuously differentiable.
- If
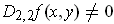 for all
for all
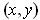 , show that
, show that
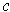 is
differentiable and
is
differentiable and
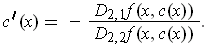
Just as in the last problem, the uniqueness condition guarantees that
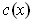 is the same as the function provided by the implicit function
theorem applied to
is the same as the function provided by the implicit function
theorem applied to
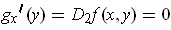 . In particular,
. In particular,
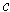 is
differentiable and differentiating this last relation gives
is
differentiable and differentiating this last relation gives
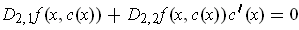 . Solving for
. Solving for
 gives the result.
gives the result.
- Show that if
 , then for some
, then for some
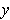 we have
we have
 and
and
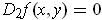 .
.
This follows immediately from part (a).
- Let
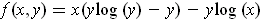 . Find
. Find
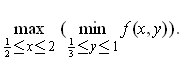
Note that
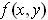 is defined only when
is defined only when
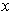 and
and
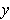 are positive. So we need
to go back and show that the earlier parts of the problem generalize to this
case; there are no difficulties in doing this.
are positive. So we need
to go back and show that the earlier parts of the problem generalize to this
case; there are no difficulties in doing this.
One has
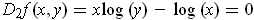 precisely when
precisely when
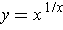 and so the hypothesis of part (a) is true and
and so the hypothesis of part (a) is true and
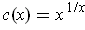 . Also,
. Also,
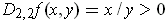 (since both
(since both
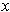 and
and
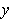 are positive), and so
for fixed
are positive), and so
for fixed
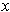 , the minimum of
, the minimum of
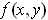 occurs at
occurs at
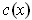 by the second
derivative test. Now actually, we are not looking for the minimum over all
by the second
derivative test. Now actually, we are not looking for the minimum over all
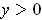 , but just for those in the interval
, but just for those in the interval
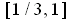 . The derivative
. The derivative
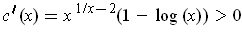 for
for
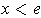 . Further
. Further
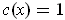 precisely when
precisely when
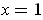 and there is a unique
and there is a unique
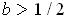 where
where
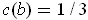 .
For fixed
.
For fixed
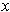 ,
,
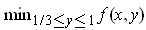 is achieved at
is achieved at
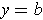 if
if
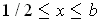 , at
, at
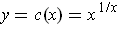 if
if
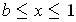 , and
at
, and
at
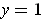 if
if
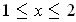 .
.
We will find where the maximum of the minimum's are located in each of the three cases.
Suppose
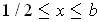 . Then we need to maximize
. Then we need to maximize
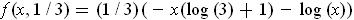 . The derivative of this function is negative
throughout the interval; so the maximum occurs at
. The derivative of this function is negative
throughout the interval; so the maximum occurs at
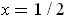 . The maximum
value is
. The maximum
value is
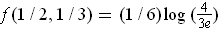 .
.
Suppose
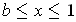 . Then
. Then
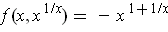 . The derivative
of this function is
. The derivative
of this function is
 . This function has
no zeros in the interval because
. This function has
no zeros in the interval because
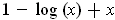 has derivative
has derivative
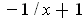 which is always negative in the interval and the value of the function is
positive at the right end point. Now
which is always negative in the interval and the value of the function is
positive at the right end point. Now
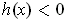 on the interval, and so
the maximum must occur at the left hand end point. The maximum value is
on the interval, and so
the maximum must occur at the left hand end point. The maximum value is
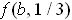 . In view of the last paragraph, that means that the maximum
over the entire interval
. In view of the last paragraph, that means that the maximum
over the entire interval
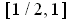 occurs at
occurs at
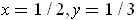 .
.
Suppose
 . Then
. Then
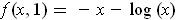 . This is a decreasing
function and so the maximum occurs at the left hand endpoint. By the
result of the previous paragraph the maximum over the entire interval
. This is a decreasing
function and so the maximum occurs at the left hand endpoint. By the
result of the previous paragraph the maximum over the entire interval
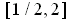 must therefore occur at
must therefore occur at
 ,
,
 , and the value of the maximum
is
, and the value of the maximum
is
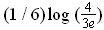 .
.