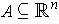 and
and
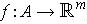 be a
function. Let
be a
function. Let
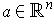 and
and
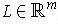 . The function
. The function
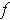 has limit
has limit
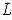 as x approaches a if for every
as x approaches a if for every
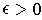 ,
there is a
,
there is a
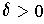 such that for every
such that for every
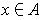 with
with
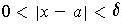 ,
one has
,
one has
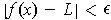 . This is expressed as
. This is expressed as
What does it mean for a function to be continuous? An elementary calculus course would define:
Definition 1: Let
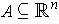 and
and
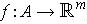 be a
function. Let
be a
function. Let
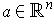 and
and
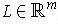 . The function
. The function
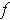 has limit
has limit
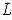 as x approaches a if for every
as x approaches a if for every
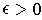 ,
there is a
,
there is a
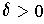 such that for every
such that for every
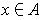 with
with
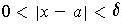 ,
one has
,
one has
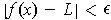 . This is expressed as
. This is expressed as
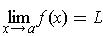
Definition 2:The function f is said to be continuous at
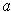 if
if
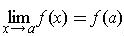
On the other hand, in a first topology course, one might define:
Definition 3: A topological space is a pair (X,
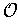 ) where
X is a set and
) where
X is a set and
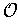 is a collection of subsets of X (called the open
sets of the topological space) such that
is a collection of subsets of X (called the open
sets of the topological space) such that
As an abbreviation, we speak of the topological space X when we don't
need to refer to
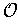 . A set is closed if its complement is open.
. A set is closed if its complement is open.
Exercise 1: If (X,
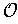 ) is a topological space and
) is a topological space and
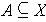 ,
then (A,
,
then (A,
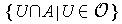 ) is also a topological space.
We say that this is the topology induced on A by the topology on X.
) is also a topological space.
We say that this is the topology induced on A by the topology on X.
Definition 4: A function
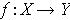 of topological spaces
is continuous if for every open subset
of topological spaces
is continuous if for every open subset
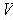 of
of
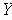 ,
,
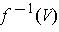 is an open subset
of X.
is an open subset
of X.
Definition 5:An open rectangle
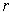 is defined to be a subset of
is defined to be a subset of
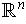 of the form
of the form
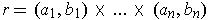 , i.e. There are real numbers
, i.e. There are real numbers
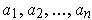 and
and
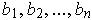 where
where
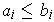 for all i
and
for all i
and
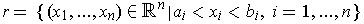
In the case of
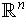 , we can define a topology by saying that a subset
, we can define a topology by saying that a subset
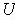 of
of
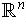 is open if every point
is open if every point
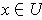 is contained in an open rectangle
is contained in an open rectangle
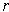 which is entirely contained in
which is entirely contained in
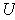 . We call this the usual topology of
. We call this the usual topology of
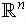 and for any subset
and for any subset
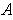 of
of
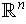 , the induced topology is called the
usual topology of
, the induced topology is called the
usual topology of
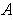 .
.
Exercise 2: Make a reasonable definition of closed rectangle. Prove that open rectangles are open sets and closed rectangles are closed sets.
Exercise 3: Instead of rectangles, we could have used open balls. Show that the resulting topology would be the same.
We are now ready for:
Proposition 1: With the usual topology on
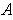 and
and
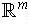 , the two
notions of continuous function are equivalent.
, the two
notions of continuous function are equivalent.
Proof: This is easy if you did Exercise 3.
The most important theorem in one variable calculus is:
Theorem 1: (Mean Value Theorem) If
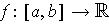 (where
(where
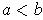 ) is continuous on
) is continuous on
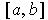 and differentiable on
and differentiable on
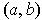 , then
there is at least one
, then
there is at least one
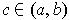 satisfying
satisfying
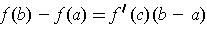
The principal ingredient of the proof of this theorem is:
Theorem 2: (Extreme Value Theorem) Every continuous function
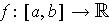 (where
(where
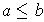 has at least one absolute
minimum and at least one absolute maximum.
has at least one absolute
minimum and at least one absolute maximum.
Usually, in an elementary calculus course, one proves the Mean Value
Theorem, but not the Extreme Value Theorem -- the second result is usually
taken to be intuitively obvious. Actually, this is a rather subtle
and difficult result. To begin with, let us note that in fact, the
Extreme Value Theorem holds when the interval
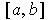 is replaced with
a closed and bounded subset of the real numbers, where bounded is defined as:
is replaced with
a closed and bounded subset of the real numbers, where bounded is defined as:
Definition 6: A subset
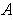 of
of
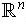 is said to be
bounded if it is contained ins ome open rectangle.
is said to be
bounded if it is contained ins ome open rectangle.
Exercise 4: Find counterexamples to Theorem 2 if you either just assume that the interval is not closed or that it is not bounded.
Definition 7: A cover for a subset
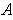 of a topological space X
is simply any collection
of a topological space X
is simply any collection
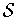 of subsets of X whose union contains
of subsets of X whose union contains
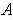 . The cover is called open (respectively finite) if the subsets are all
open (respectively are finite in number).
. The cover is called open (respectively finite) if the subsets are all
open (respectively are finite in number).
Definition 8: A subset A of a topological space X is said to be compact if every open cover of A contains a finite subcover (i.e. a finite subset of the cover is itself a cover).
Proposition 2: If
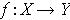 is continuous and
is continuous and
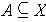 is compact, then so is
is compact, then so is
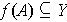 .
.
Proof: If
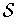 is an open cover of
is an open cover of
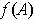 , then
, then
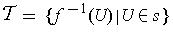 is an open cover of A (Why?).
Since
is an open cover of A (Why?).
Since
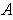 is compact,
is compact,
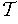 has a finite subcover,
say
has a finite subcover,
say
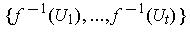 , where the
, where the
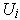 are all in
are all in
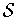 .
Now, one can verify that
.
Now, one can verify that
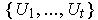 form a finite cover of
form a finite cover of
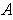 .
.
Exercise 5: With the usual topology on
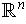 , if
, if
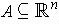 is compact, then
is compact, then
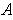 is both closed and bounded.
is both closed and bounded.
Theorem 5: (Heine-Borel Theorem) With the usual topology on
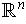 ,
a subset
,
a subset
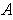 of
of
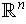 is compact if and only if it both closed and bounded.
is compact if and only if it both closed and bounded.
Note: The Extreme Value Theorem follows: If
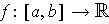 is continuous, then
is continuous, then
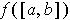 is the image of a compact set and so is compact
by Proposition 2. So, it is both closed and bounded by Exercise 5. In
particular, the least upper bound of
is the image of a compact set and so is compact
by Proposition 2. So, it is both closed and bounded by Exercise 5. In
particular, the least upper bound of
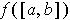 (which exists by the
completeness property of the real numbers) is in
(which exists by the
completeness property of the real numbers) is in
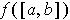 (Why?). So,
(Why?). So,
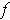 has an absolute maximum.
has an absolute maximum.
The Heine-Borel Theorem can be proved in at least two ways. The first method proceeds by building up larger and larger sets which are known to be compact. One starts with Lemma 1 below and then uses Lemma 2 to inductively conclude that any closed rectangle is compact. Finally, Lemma 3 completes the proof.
Lemma 1: A closed interval
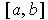 is compact.
is compact.
Proof: Let
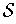 be an open cover of
be an open cover of
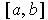 (assumed
non-empty). The set
(assumed
non-empty). The set
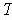 of all
of all
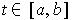 such that
such that
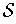 contains
a finite subcover of
contains
a finite subcover of
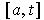 is bounded. So it has a least upper bound, say
is bounded. So it has a least upper bound, say
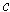 .
Let
.
Let
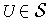 contain
contain
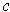 and hence an open interval
and hence an open interval
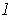 containing
containing
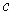 .
Choose
.
Choose
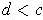 in this open interval. Then
in this open interval. Then
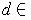 and so there is a finite
subcover
and so there is a finite
subcover
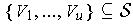 of
of
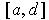 . But then
. But then
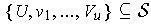 is a finite subcover of
is a finite subcover of
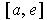 for
any
for
any
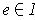 contrary to the choice of
contrary to the choice of
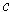 .
.
Lemma 2: If
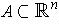 and
and
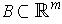 are compact, then so is
are compact, then so is
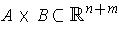 .
.
Proof: Suppose
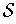 is an open cover of
is an open cover of
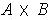 .
If
.
If
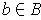 ,
,
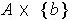 is compact. Further,
is compact. Further,
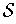 is also an open cover of
is also an open cover of
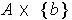 and so this set has a finite subcover
and so this set has a finite subcover
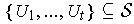 .
For every
.
For every
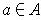 , there is an open rectangle
, there is an open rectangle
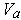 containing
containing
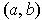 and contained
in some one of the
and contained
in some one of the
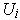 ; the set of these is rectangles is an open cover of
; the set of these is rectangles is an open cover of
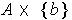 and so admits of an open subcover
and so admits of an open subcover
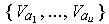 of the same set. Each rectangle
of the same set. Each rectangle
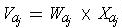 where
where
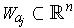 and
and
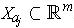 are open
rectangles. Letting
are open
rectangles. Letting
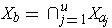 , it follows that
, it follows that
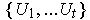 is actually a finite open cover of
is actually a finite open cover of
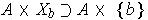 .
.
For each
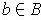 , we can do the construction of the last paragraph. The
set of all the
, we can do the construction of the last paragraph. The
set of all the
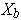 for all the
for all the
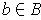 is an open cover of
is an open cover of
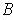 and so it
admits of a finite subcover
and so it
admits of a finite subcover
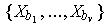 . But then the set of
all the
. But then the set of
all the
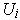 's associated with all the
's associated with all the
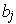 's is a finite subcover of
's is a finite subcover of
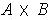 .
.
Lemma 3: If every rectangle is compact, then every closed and bounded
subset of
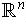 is compact.
is compact.
Proof: If
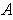 is closed and bounded, then it is contained in
a closed rectangle
is closed and bounded, then it is contained in
a closed rectangle
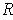 . If
. If
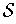 is an open cover of
is an open cover of
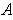 , then adding
the complement of
, then adding
the complement of
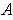 in
in
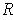 to the cover gives an open cover of
to the cover gives an open cover of
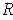 . Since
. Since
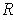 is compact, there is a finite subcover. But then after possibly removing
the complement of
is compact, there is a finite subcover. But then after possibly removing
the complement of
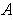 in
in
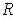 , we get a finite subcover of
, we get a finite subcover of
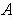 .
.
The second proof of the Heine-Borel Theorem proceeds by binary search. We will prove it in the case an interval and leave the generalization to a rectangle as an exercise.
Proof:(Heine-Borel, case where
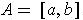 ) Suppose the result is false. Then there
is an open cover
) Suppose the result is false. Then there
is an open cover
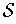 of
of
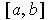 without a finite subcover. Let's look for
smaller intervals with the same property with respect to this fixed cover.
Clearly, either the left or the right half of
without a finite subcover. Let's look for
smaller intervals with the same property with respect to this fixed cover.
Clearly, either the left or the right half of
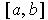 must not have a finite
subcover (Otherwise, the union of the subcovers for each half would give a
subcover for the whole interval.) We can now apply the same reasoning to
a half that does not have a finite subcover, etc. This gives a sequence
of intervals
must not have a finite
subcover (Otherwise, the union of the subcovers for each half would give a
subcover for the whole interval.) We can now apply the same reasoning to
a half that does not have a finite subcover, etc. This gives a sequence
of intervals
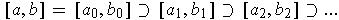
where
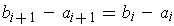 for every
for every
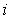 and such that each
subinterval does not admit of a finite subcover of
and such that each
subinterval does not admit of a finite subcover of
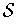 . Clearly,
one has
. Clearly,
one has
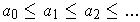 . Let
. Let
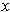 be the least upper bound of
the set of these
be the least upper bound of
the set of these
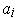 . Then
. Then
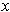 is in
is in
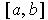 and so there is a set
and so there is a set
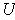 in
in
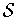 with
with
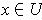 . It is now easy to see that
. It is now easy to see that
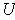 contains
almost all the intervals
contains
almost all the intervals
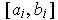 , which is a contradiction.
, which is a contradiction.
Exercise 6: Generalize the above proof to show that every closed
rectangle in
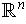 is compact.
is compact.
Definition 9: The derivative of the function
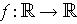 is
is
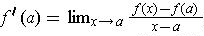 whenever it exists.
whenever it exists.
Proposition 3: With
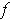 as in the definition, suppose that the
derivative of
as in the definition, suppose that the
derivative of
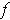 at
at
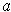 exists. If
exists. If
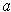 is a local maximum or local minimum
of
is a local maximum or local minimum
of
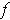 , then the derivative of
, then the derivative of
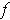 at
at
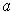 is zero.
is zero.
Proof:Suppose, for example, that
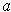 is a local maximum of
is a local maximum of
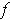 ,
i.e.
,
i.e.
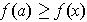 for all
for all
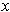 in an open interval containing
in an open interval containing
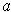 . But then
for
. But then
for
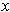 in this interval with
in this interval with
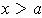 , one has
, one has
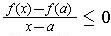 and so the limit as
and so the limit as
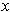 approaches
approaches
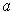 from the right must be non-positive.
By taking
from the right must be non-positive.
By taking
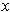 in the interval with
in the interval with
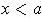 , one has
, one has
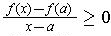 and so the limit as
and so the limit as
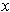 approaches
approaches
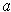 from the left must be non-negative. If
the limit exists, then these two must be equal, and so the derivative is zero.
The proof in case of a local minimum is analogous.
from the left must be non-negative. If
the limit exists, then these two must be equal, and so the derivative is zero.
The proof in case of a local minimum is analogous.
Proposition 4: (Rolle's Theorem) If
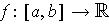 is continuous on
is continuous on
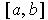 and differentiable on
and differentiable on
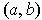 and
and
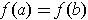 , then
for some
, then
for some
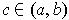 , one has
, one has
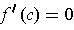 .
.
Proof: If the result is false, then Proposition 3 says that there
is no local maximum or local minimum in
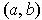 . On the other hand, the
Extreme Value Theorem says that there is at least one absolute maximum and
at least one absolute minimum; so both must be at the endpoints. But, then
the function must be constant in the entire interval. This is a contradiction.
. On the other hand, the
Extreme Value Theorem says that there is at least one absolute maximum and
at least one absolute minimum; so both must be at the endpoints. But, then
the function must be constant in the entire interval. This is a contradiction.
We can now prove:
Corollary 1: (Mean Value Theorem) If
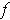 and
and
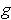 are both real valued
functions continuous on
are both real valued
functions continuous on
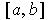 and differentiable on
and differentiable on
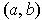 and if the
graphs of
and if the
graphs of
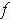 and
and
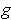 intersect at
intersect at
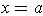 and
and
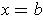 , then
there is at least one
, then
there is at least one
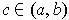 satisfying
satisfying
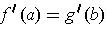 .
.
Proof: Apply Rolle's Theorem to the function
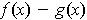 .
.
Note: Theorem 1 is the special case where
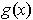 is the straight
line from
is the straight
line from
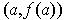 to
to
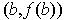 .
.
Corollary 2: (Taylor's Theorem with Remainder) Let
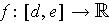 and its first n derivatives be continuous on
and its first n derivatives be continuous on
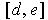 and
and
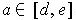 .
Then for all
.
Then for all
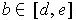 , one has:
, one has:
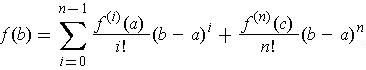
for some
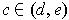 .
.
Proof: Consider the function:
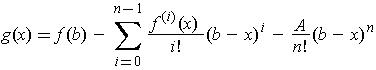
where the constant A is chosen so that
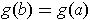 . The derivative can
be calculated using the product rule:
. The derivative can
be calculated using the product rule:
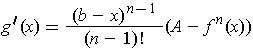
Using Rolle's Theorem, we know that there is a
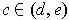 satisfying
satisfying
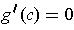 ;
this is the
;
this is the
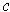 we are looking for.
we are looking for.