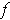 , the change from
, the change from
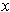 to
to
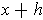 is
is
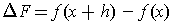 .
For example, if
.
For example, if
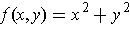 , then the change in going from
, then the change in going from
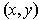 to
to
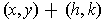 is
is
Given a function
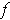 , the change from
, the change from
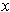 to
to
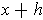 is
is
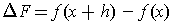 .
For example, if
.
For example, if
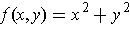 , then the change in going from
, then the change in going from
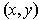 to
to
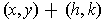 is
is
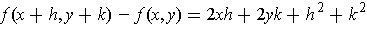
This can be seen as a linear function
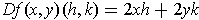 plus another
part
plus another
part
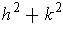 which is small in the sense that
which is small in the sense that
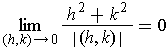
Definition 1: If
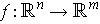 is a
function, then a derivative
is a
function, then a derivative
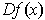 of
of
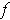 at
at
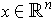 is a
linear function from
is a
linear function from
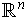 to
to
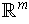 such that
such that

Proposition 1: There is at most one derivative of
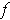 at
at
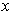 .
.
Proof: Suppose that
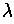 and
and
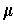 are two derivatives.
Then each satisfies the limit condition of the definition. Subtracting
these gives:
are two derivatives.
Then each satisfies the limit condition of the definition. Subtracting
these gives:
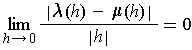
For
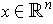 , let
, let
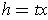 for
for
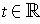 . Then
. Then
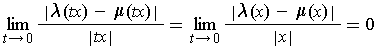
since
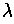 and
and
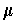 are linear. So
are linear. So
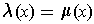
Exercise 1: If
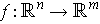 is
linear, then
is
linear, then
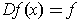 for all
for all
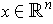 . If
. If
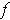 is a constant
function, then
is a constant
function, then
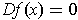 for all
for all
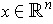 .
.
Proposition 2: If
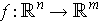 and
and
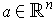 , then
, then
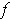 is differentiable at
is differentiable at
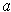 if and only if
the coordinate functions
if and only if
the coordinate functions
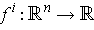 are
differentiable for all
are
differentiable for all
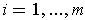 . If either is true, then
. If either is true, then
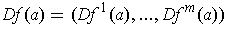 .
.
Proof: If
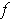 is differentiable at
is differentiable at
 , then
, then
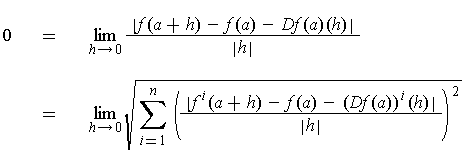
In particular each of the terms of the sum have limit zero. So the
coordinate functions
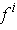 have derivatives and they are the coordinate functions of the
derivative of
have derivatives and they are the coordinate functions of the
derivative of
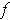 . Conversely, if the coordinate functions
. Conversely, if the coordinate functions
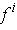 are
differentiable, then putting their derivatives in the above formula in the
place of the coordinate functions of
are
differentiable, then putting their derivatives in the above formula in the
place of the coordinate functions of
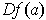 shows that
shows that
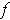 is differentiable
at
is differentiable
at
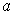 .
.
The main computational tool for derivatives is:
Theorem 1: (Chain Rule) If
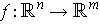 is differentiable at
is differentiable at
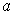 and if
and if
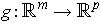 is differentiable at
is differentiable at
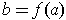 , then
, then
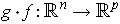 is differentiable at
is differentiable at
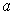 and
and
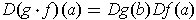 .
.
Proof: Define
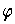 and
and
 by
by
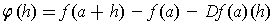
and
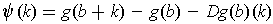
We need to show that
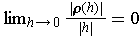 where
where
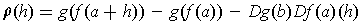
Now, letting
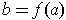 and
and
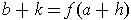 , we have by the definition of
, we have by the definition of
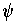 ,
,
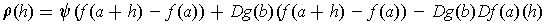
Using the definition of
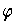 , we get
, we get
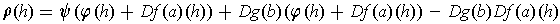
By linearity of
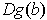 , this simplifies to:
, this simplifies to:
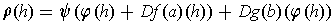
We must show that
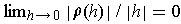 . Since
. Since
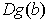 is
linear, there is an
is
linear, there is an
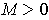 such that
such that
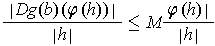
and the right hand side approaches zero.
For the other term, for any
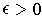 ,
there is a
,
there is a
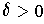 such that
such that
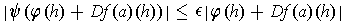
whenever
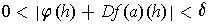 . Note that we can remove the
condition that the middle term be non-zero -- if it were zero, then
the condition becomes
. Note that we can remove the
condition that the middle term be non-zero -- if it were zero, then
the condition becomes
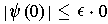 which is true since
which is true since
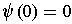 . Now
. Now
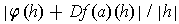 is bounded for small
is bounded for small
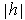 .
So
.
So
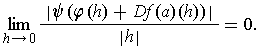
This completes the proof.
Corollary 1: If
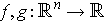 are
differentiable at
are
differentiable at
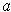 , then
, then
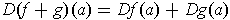
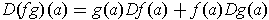
Proof: The sum
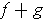 (respectively the product
(respectively the product
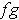 ) function can be
written as the composition of the
) function can be
written as the composition of the
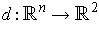 defined by
defined by
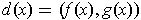 and the function
and the function
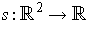 (respectively
(respectively
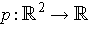 ) defined by
) defined by
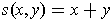 (respectively
(respectively
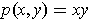 ). Now
). Now
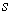 is linear and
so its derivative is itself. Further, it is easy to check that:
is linear and
so its derivative is itself. Further, it is easy to check that:
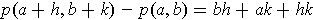
and so
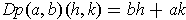 since
since
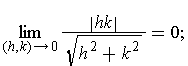
The formulas now follow by the chain rule.
Definition 2: Let
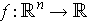 be a function and
be a function and
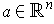 .
Then, for each j, one can define
.
Then, for each j, one can define
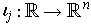 by
by
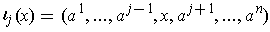 . The
. The
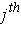 partial
derivative
partial
derivative
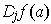 of
of
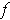 at
at
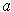 is defined to be
is defined to be
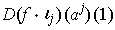 .
.
Proposition 3: Let
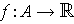 be a function with domain
be a function with domain
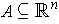 and
and
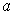 be in the interior of
be in the interior of
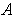 and assume that
and assume that
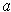 is either a local minimum or local maximum of
is either a local minimum or local maximum of
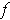 . Then
. Then
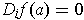 provided that the partial derivative exists.
provided that the partial derivative exists.
Proof:
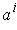 is a local extremum of the function of one variable
is a local extremum of the function of one variable
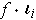 .
.
Theorem 2: Let
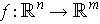 be a function and
be a function and
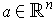 . If
. If
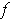 is differentiable at
is differentiable at
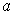 , then
, then
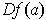 is the
linear transformation whose matrix is the
is the
linear transformation whose matrix is the
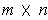 array of
partial derivatives
array of
partial derivatives
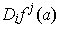 of the coordinate functions
of the coordinate functions
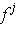 of
of
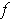 .
Conversely, if The partial derivatives of the coordinate functions of
.
Conversely, if The partial derivatives of the coordinate functions of
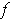 all have partials defined in an open neighborhood of
all have partials defined in an open neighborhood of
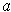 and are continuous
at
and are continuous
at
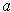 , then
, then
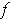 is differentiable at
is differentiable at
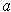 .
.
Proof: By Proposition 2, it is enough to check the case where
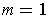 .
The first assertion is immediate from the definitions. For the
second assertion break up the change in
.
The first assertion is immediate from the definitions. For the
second assertion break up the change in
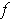 into a sum of changes in which
one varies only one parameter at a time:
into a sum of changes in which
one varies only one parameter at a time:
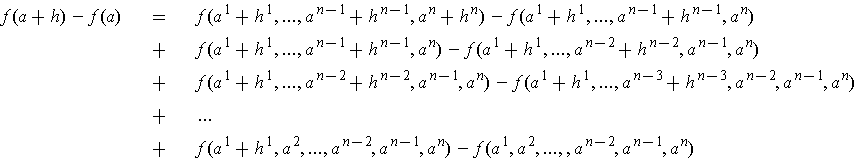
One can apply the Mean Value Theorem to each of the differences on the right:
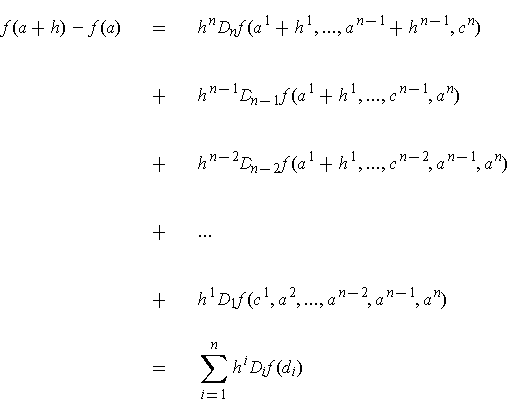
where
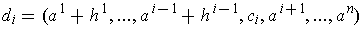 .
It follows that
.
It follows that
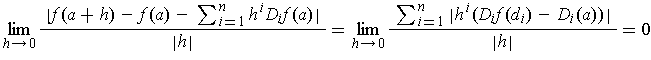
because the
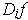 are continuous at
are continuous at
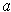 .
.
Corollary 2: (Chain Rule) If
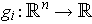 for
for
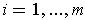 are
continuously differentiable at
are
continuously differentiable at
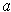 and if
and if
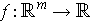 is
differentiable at (g_1(a),...,g_m(a)), then
is
differentiable at (g_1(a),...,g_m(a)), then
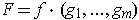 has
partial derivatives
has
partial derivatives
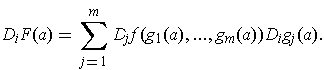
Proof: Apply the Chain Rule and Theorem 2.
Theorem 3: If
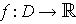 is a function defined on
an open subset
is a function defined on
an open subset
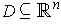 and if
and if
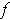 and its first and
second order partials are exist throughout
and its first and
second order partials are exist throughout
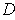 and are continuous there,
then
and are continuous there,
then
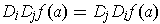 for all
for all
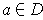 .
.
Proof: It is clearly enough to prove the result in the case where
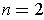 . Let
. Let
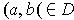 and
and
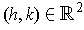 be such that the rectangle
with diagonal from
be such that the rectangle
with diagonal from
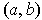 to
to
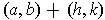 is contained in
is contained in
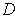 .
Let
.
Let
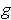 be defined by
be defined by
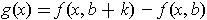 . First apply the
Mean Value Theorem to find a
. First apply the
Mean Value Theorem to find a
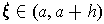 such that
such that
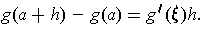
Now,
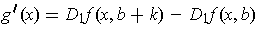 . Apply the Mean Value Theorem again
to find
. Apply the Mean Value Theorem again
to find
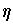 between
between
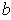 and
and
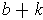 such that
such that
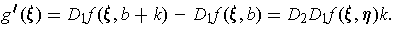
Combining results we have
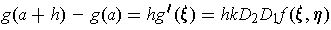
But
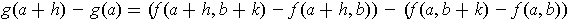
which is symmetric in the two variables. So, one can obtain another
expression for the same by repeating the same construction swapping the
roles of the two variables: Let
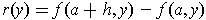 and get
and get
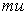 and
and
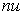 such that
such that
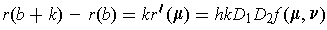
and
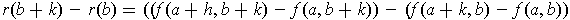
So
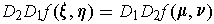 . Now take the limit as
. Now take the limit as
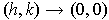 and use the continuity of the second partials to conclude
that the mixed partials are equal.
and use the continuity of the second partials to conclude
that the mixed partials are equal.