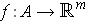 be defined and differentiable
on a convex open set A. Then for all
be defined and differentiable
on a convex open set A. Then for all
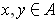 , one has
, one has
Lemma 1: Let
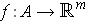 be defined and differentiable
on a convex open set A. Then for all
be defined and differentiable
on a convex open set A. Then for all
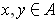 , one has
, one has
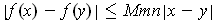
where
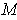 is chosen to be an upper bound on all the
is chosen to be an upper bound on all the
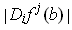 for all
for all
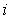 ,
,
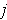 , and all
, and all
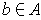 .
.
Proof: Let
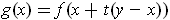 . For each
. For each
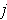 , the Mean Value
Theorem says that there is a
, the Mean Value
Theorem says that there is a
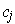 between 0 and 1 such that
between 0 and 1 such that
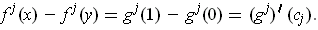
By the chain rule,
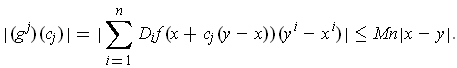
So,
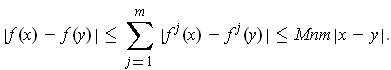
Theorem 1: (Inverse Function Theorem) Let
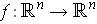 be continuously differentiable on an open subset containing
be continuously differentiable on an open subset containing
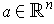 .
If
.
If
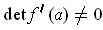 , then there are open subsets
, then there are open subsets
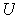 containing
containing
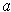 and
and
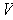 containing
containing
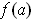 such that
such that
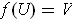 and there is an inverse
and there is an inverse
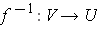 which is differentiable with derivative satisfying:
which is differentiable with derivative satisfying:
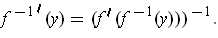
Exercise 1: Show that Theorem 1 is true for linear functions.
Proof: (of Theorem 1) By replacing
 with
with
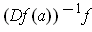 , we
can assume that
, we
can assume that
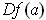 is the identity map (Why?).
is the identity map (Why?).
Apply Lemma 1 to
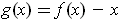 :
:
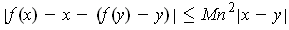 for
for
 and
and
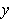 in some open rectangle containing
in some open rectangle containing
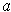 . But then,
. But then,
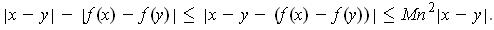
Rearranging gives
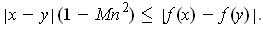
Since
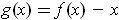 ,
,
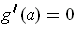 and so by choosing the rectangle
small enough, we can assume that
and so by choosing the rectangle
small enough, we can assume that
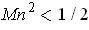 and so
and so
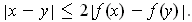
In particular, it follows that f is one-to-one when restricted to this
rectangle, and the inverse will be continuous if it exists.
Replacing the rectangle with a smaller one, we can assume the
same is true when f is restricted to the closure of the rectangle. Now
the boundary
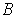 of the rectangle is compact and so
of the rectangle is compact and so
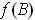 is also compact
and does not contain
is also compact
and does not contain
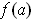 . Let
. Let
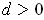 be the minimum of
be the minimum of
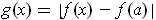 for
for
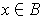 . Let
. Let
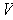 be the set
be the set
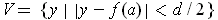 .
.
Now, for every
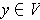 , there is at least one
, there is at least one
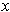 in the rectangle with
in the rectangle with
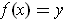 . In fact, consider the function
. In fact, consider the function
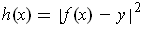 . The
image of
. The
image of
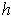 under the closure of the rectangle. The minimum of this
function does not occur on
under the closure of the rectangle. The minimum of this
function does not occur on
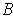 because
because
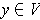 . So it must occur where
the derivative is zero, i.e. one has:
. So it must occur where
the derivative is zero, i.e. one has:
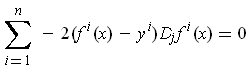
for
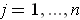 . But by taking the rectangle sufficiently small, we can
assume that
. But by taking the rectangle sufficiently small, we can
assume that
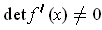 for all
for all
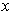 in the rectangle. But then
the only solution of this system of linear equations is
in the rectangle. But then
the only solution of this system of linear equations is
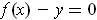 .
.
If
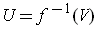 , then
, then
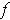 maps the open set
maps the open set
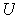 one-to-one and onto
the open set
one-to-one and onto
the open set
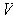 . It remains to check differentiability of the inverse.
Since
. It remains to check differentiability of the inverse.
Since
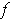 is differentiable, one has for
is differentiable, one has for
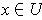 ,
,
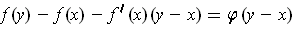
where
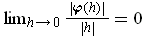 . Letting
. Letting
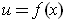 and
and
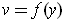 , we get after substitution:
, we get after substitution:
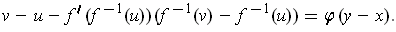
Rearranging gives:
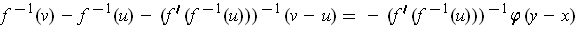
It remains to show that
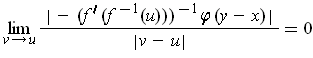
Since the derivative is just a linear function, it is enough to show that
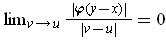 . As
. As
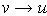 , we have
, we have
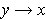 because
because
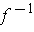 is continuous. So,
is continuous. So,
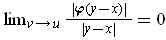 .
But we know that
.
But we know that
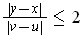 So, the limit of the product
is zero, as desired.
So, the limit of the product
is zero, as desired.
Note: It follows from the formula for the derivative of the inverse that the inverse is also continuously differentiable.
Corollary 1: (The Implicit Function Theorem) Let
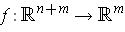 be continuously differentiable in an open set containing the point
be continuously differentiable in an open set containing the point
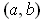 which satisfies
which satisfies
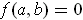 . Suppose that
. Suppose that
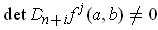 .
Then there is a continuously differentiable function
.
Then there is a continuously differentiable function
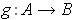 mapping
an open set
mapping
an open set
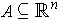 containing
containing
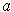 to an open set
to an open set
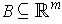 containing
containing
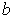 such that
such that
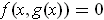 for all
for all
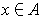 .
.
Proof: We can extend
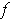 to a function
to a function
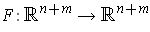 by
by
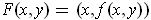 and apply the Inverse Function Theorem to get
an inverse
and apply the Inverse Function Theorem to get
an inverse
 defined in an open subset containing
defined in an open subset containing
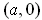 and mapping onto
an open subset containing
and mapping onto
an open subset containing
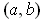 . Let
. Let
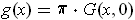 where
where
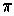 is the projection onto the last
is the projection onto the last
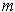 coordinates of
coordinates of
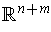 .
Then one has
.
Then one has
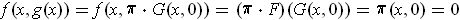 .
.
Exercise 2: Show that the Inverse Function Theorem is a Corollary of the Implicit Function Theorem.