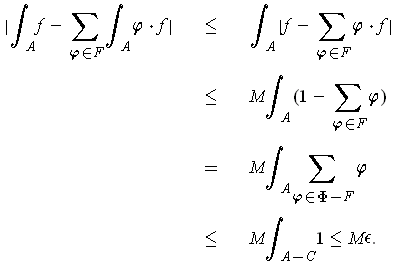of
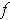 for the partition
for the partition
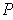 are defined to be
are defined to be
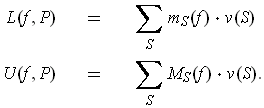
The definitions have been constructed to make the following trivial, but
crucial Lemma true.
Lemma 1: With the notation as in Definition 1, every subrectangle
of
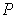 is a union of finitely many subrectangles of
is a union of finitely many subrectangles of
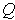 whose interiors are
pairwise disjoint. As a result, one has:
whose interiors are
pairwise disjoint. As a result, one has:
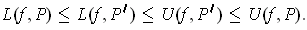
Definition 2: With the notation as in Definition 1, the lower
integral (respectively upper integral of
 on
on
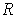 is defined
to be
is defined
to be
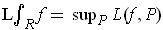 (respectively
(respectively
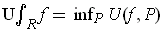 ). If
). If
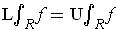 ,
then
,
then
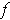 is called integrable with integral
is called integrable with integral
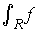 equal to this
common value. Another notation for the integral is
equal to this
common value. Another notation for the integral is
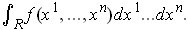
Proposition 1: A bounded function
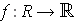 defined on
a rectangle
defined on
a rectangle
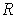 is integrable if and only if for every
is integrable if and only if for every
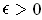 ,
there is a partition
,
there is a partition
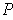 such that
such that
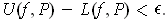
Proof: The condition is clearly sufficient. On the other hand,
if
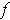 is integrable and
is integrable and
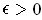 , then there are partitions
, then there are partitions
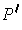 and
and
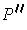 such that
such that
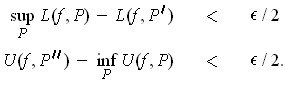
Let
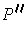 be a refinement of both
be a refinement of both
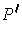 and
and
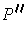 . Then Lemma 1 implies that
. Then Lemma 1 implies that
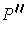 is a partition of the desired type.
is a partition of the desired type.
Theorem 1: (Fubini's Theorem) Let
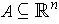 and
and
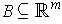 be closed rectangles and
be closed rectangles and
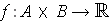 be integrable. For
be integrable. For
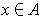 , let
, let
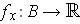 be defined by
be defined by
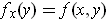 and let
and let
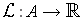 and
and
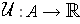 be defined by:
be defined by:
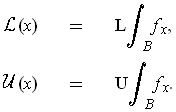
Then
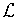 and
and
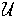 are both integrable on
are both integrable on
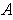 and
and
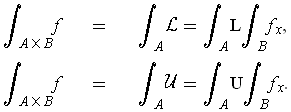
In other words, the double integral can be calculated as either of
two iterated integrals:
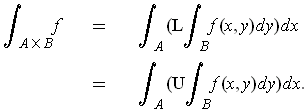
Proof: This is mostly a matter of sorting out all the definitions.
If
 (respectively
(respectively
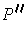 ) is a partition of
) is a partition of
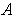 (respectively
(respectively
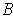 ), then
), then
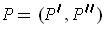 is a partition of
is a partition of
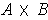 with subrectangles of the
form
with subrectangles of the
form
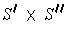 where
where
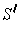 is a subrectangle of
is a subrectangle of
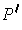 and
and
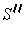 is a
subrectangle of
is a
subrectangle of
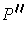 .
.
One has:
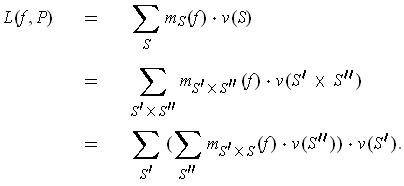
For
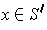 , one has
, one has
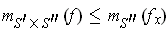 , and so
, and so
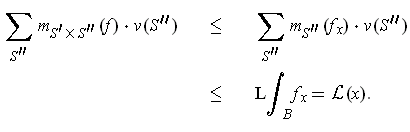
But then:
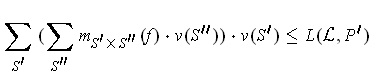
and so, combining results, we get:
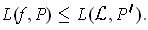
For the upper sums, one can argue analogously:
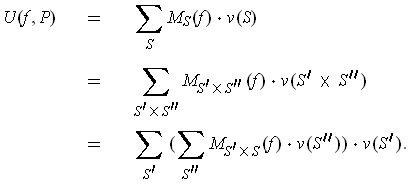
For
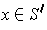 , one has
, one has
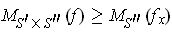 , and so
, and so
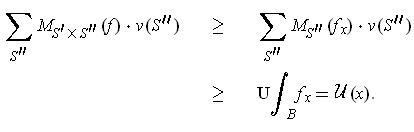
But then:
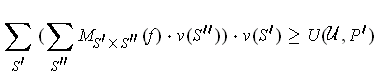
and so, combining results, we get:
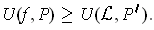
Combining the results for upper and lower sums:
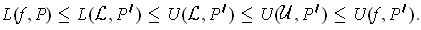
Since
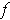 is integrable,
is integrable,
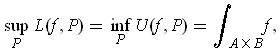
and so
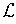 is integrable with integral equal to
is integrable with integral equal to
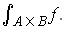
A similar argument shows that
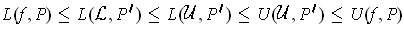
and so one gets
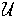 is integrable with integral
is integrable with integral
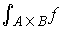 ,
as desired.
,
as desired.
Note: By interchanging the roles of
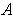 and
and
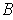 , one can show that
the order in which the integrals are iterated does not affect the result.
, one can show that
the order in which the integrals are iterated does not affect the result.
Extending the Integral: Characteristic Functions
Exercise 1: State and prove a result which would make the following
definition legitimate and reasonable.
Definition 3: If
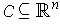 , then its characteristic
function
, then its characteristic
function
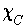 is defined by
is defined by
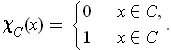
If
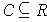 where
where
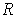 is a closed rectangle, then a bounded function
is a closed rectangle, then a bounded function
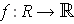 is said to be integrable with integral
is said to be integrable with integral
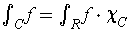 provided that this last quantity is defined.
provided that this last quantity is defined.
Definition 4: A subset
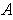 of
of
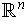 is said to be of
measure zero (respectively content zero) if for every
is said to be of
measure zero (respectively content zero) if for every
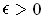 ,
there is a countable infinite (respectively finite) sequence
,
there is a countable infinite (respectively finite) sequence
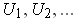 of open rectangles which form a cover of
of open rectangles which form a cover of
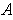 and such that
and such that
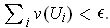
Exercise 2: Show that, if we replace open with closed
in Definition 4, the resulting definitions are equivalent.
Proposition 2: (i) The union of a countable collection of sets of
measure zero is also of measure zero.
(ii) A compact set is of measure zero if and only if it is of content zero.
(iii) A closed interval
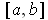 with
with
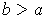 is not of measure zero.
is not of measure zero.
Proof: (i) Suppose
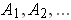 is a countable sequence of
sets of measure zero and
is a countable sequence of
sets of measure zero and
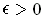 . Then
. Then
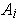 has an open cover by
rectangles
has an open cover by
rectangles
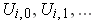 such that
such that
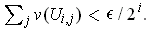 Then clearly the
Then clearly the
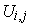 are a cover of the union of
are a cover of the union of
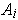 and the sum of
their volumes is less than
and the sum of
their volumes is less than
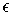 (why?). To enumerate the
(why?). To enumerate the
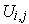 , just
list them out in order of increasing
, just
list them out in order of increasing
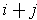 keeping those with the same value of
keeping those with the same value of
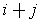 in order of increasing
in order of increasing
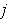 .
.
(ii> Clearly, the condition is sufficent. On the other hand, if
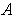 is compact and of measure 0, with an open covering
is compact and of measure 0, with an open covering
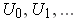 of open
rectangles of total volume less than
of open
rectangles of total volume less than
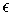 . Then any finite subcover
satisfies the same condition. So
. Then any finite subcover
satisfies the same condition. So
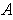 is also of content zero.
is also of content zero.
(iii) If
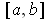 were of measure zero, it would be of content zero by
part (ii). Suppose
were of measure zero, it would be of content zero by
part (ii). Suppose
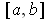 has a cover
has a cover
 by closed rectangles of
total length less than
by closed rectangles of
total length less than
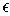 . We can replace the
. We can replace the
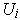 with their
intersections with
with their
intersections with
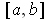 to show that the
to show that the
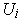 can be assumed to be
subintervals of
can be assumed to be
subintervals of
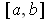 . But then the endpoints of the
. But then the endpoints of the
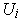 can be arranged
into increasing order to obtain a partition of
can be arranged
into increasing order to obtain a partition of
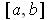 . Each
. Each
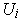 is
a union of certain of the subrectangles of this partition and so
is
a union of certain of the subrectangles of this partition and so
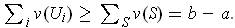 So, if
So, if
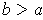 , the interval
, the interval
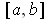 cannot be of content zero and so it is also not of measure zero.
cannot be of content zero and so it is also not of measure zero.
Definition 5: Let
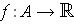 be a bounded function and
be a bounded function and
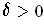 .
Define the functions:
.
Define the functions:
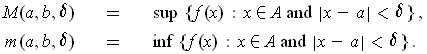
The oscillation
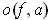 of
of
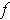 at
at
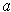 is defined to be
is defined to be
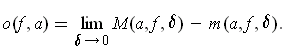
Proposition 3:(i) The bounded function
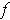 is continuous at
is continuous at
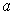 if
and only if
if
and only if
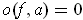 .
.
(ii) If
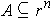 is closed,
is closed,
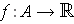 is
bounded, and
is
bounded, and
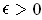 , then
, then
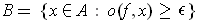 is closed.
is closed.
(iii) If
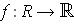 is a bounded function defined on a closed
rectangle
is a bounded function defined on a closed
rectangle
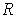 and
and
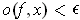 for some
for some
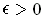 , then
there is a partition
, then
there is a partition
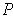 of
of
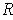 such that
such that
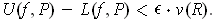
Proof: (i) Do this as an exercise.
(ii) If
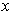 is not in
is not in
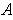 , then there is an open an open ball of radius
, then there is an open an open ball of radius
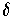 about
about
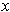 which is disjoint from
which is disjoint from
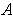 . Using this ball, one can check that
. Using this ball, one can check that
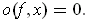 So
So
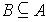 .
.
Suppose
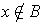 and
and
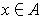 . Then
. Then
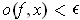 . Choose a
. Choose a
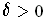 such that
such that
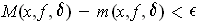 . Then for all
. Then for all
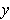 such that
such that
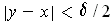 , we have
, we have
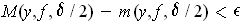 .
and so
.
and so
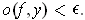 . Thus the complement of
. Thus the complement of
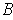 is open and
is open and
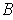 is
closed.
is
closed.
(iii) For each
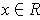 there is a closed rectangle with
there is a closed rectangle with
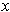 in its interior
such that
in its interior
such that
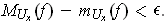 Since
Since
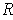 is compact, a
finite number of these are such that their interiors cover
is compact, a
finite number of these are such that their interiors cover
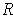 . Choose for
. Choose for
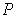 any partition of
any partition of
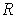 such that every subrectangle
such that every subrectangle
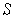 of
of
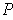 is contained in one
of these finitely many
is contained in one
of these finitely many
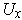 's. Then
's. Then
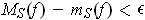 for each
subrectangle
for each
subrectangle
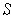 . It follows that
. It follows that
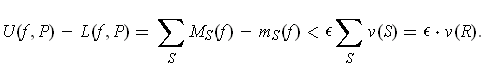
Theorem 2: Let
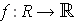 be a bounded function defined
on a closed rectangle
be a bounded function defined
on a closed rectangle
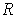 and let
and let
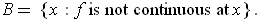 Then
Then
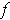 is integrable if and only if
is integrable if and only if
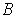 is a set of measure zero.
is a set of measure zero.
Proof: Suppose
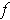 is integrable and
is integrable and
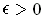 . For
. For
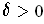 ,
choose a partition
,
choose a partition
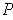 of
of
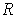 such that
such that
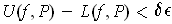 .
Then the set of subrectangles
.
Then the set of subrectangles
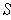 of
of
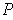 such that
such that
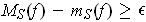 has total volume less than
has total volume less than
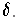 If
If
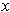 is a point where the oscillation of
is a point where the oscillation of
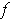 is
at least
is
at least
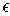 and if
and if
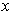 is in the interior of one of the subrectangles
of
is in the interior of one of the subrectangles
of
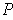 , then
, then
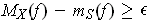 . Since the boundaries of the
subrectangles of
. Since the boundaries of the
subrectangles of
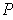 is a set of measure zero, it follows that the set
is a set of measure zero, it follows that the set
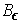 of
of
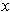 with
oscillation at least
with
oscillation at least
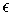 must be a set of content (and hence measure) zero.
Since the set of discontuities of the function
must be a set of content (and hence measure) zero.
Since the set of discontuities of the function
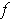 is just the union of the
countably many sets
is just the union of the
countably many sets
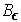 for
for
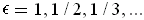 , it follows
that the set of discontinuities of
, it follows
that the set of discontinuities of
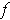 is also of measure zero.
is also of measure zero.
Now, suppose that the set of discontinuities of
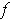 is of measure 0.
As before, let
is of measure 0.
As before, let
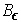 be the set of
be the set of
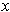 satisfying
satisfying
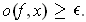 Since
Since
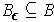 is compact by Proposition 3 and
is compact by Proposition 3 and
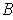 is of
measure zero,
is of
measure zero,
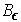 is of content zero. In particular, there is
a finite set of closed rectangles whose interiors cover
is of content zero. In particular, there is
a finite set of closed rectangles whose interiors cover
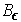 and such that their
total volume is at most
and such that their
total volume is at most
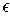 . First choose a partition
. First choose a partition
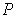 of
of
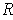 such
that every subrectangle of
such
that every subrectangle of
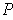 is either completely contained with one of
the finitely many rectangles or else its interior is disjoint from all of these
rectangles. For each rectangle of the first type, one has
is either completely contained with one of
the finitely many rectangles or else its interior is disjoint from all of these
rectangles. For each rectangle of the first type, one has
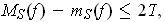 where
where
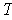 is an upper bound for |f(x)| for all
is an upper bound for |f(x)| for all
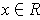 .
For each subrectangle S of the second type, one can use Proposition 3(iii)
to find a partition of the subrectangle such that the difference between
the upper and lower sums on this subrectangle is at most
.
For each subrectangle S of the second type, one can use Proposition 3(iii)
to find a partition of the subrectangle such that the difference between
the upper and lower sums on this subrectangle is at most
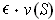 .
Now replace P with a refinement of each of these partitions. Then we
have
.
Now replace P with a refinement of each of these partitions. Then we
have
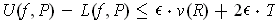 .
By making
.
By making
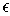 sufficiently small, we can make this sum as small as we like, and so
sufficiently small, we can make this sum as small as we like, and so
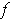 is integrable.
is integrable.
Corollary 1: Let
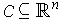 be a bounded set. Then
its characteristic function
be a bounded set. Then
its characteristic function
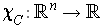 is
integrable if and only if the boundary of
is
integrable if and only if the boundary of
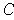 is of measure zero.
is of measure zero.
Proof: Apply Theorem 2 given that the set of discontinuities of
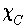 is precisely the boundary of
is precisely the boundary of
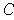 .
.
Definition 6: A bounded set
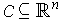 is called
Jordan measurable if its boundary is of measure zero. In this
case, the integral of its characteristic function is called
the content of
is called
Jordan measurable if its boundary is of measure zero. In this
case, the integral of its characteristic function is called
the content of
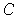 or its (n-dimensional) volume.
or its (n-dimensional) volume.
Note: Although our extension was defined in a natural way, it
is not quite adequate. Indeed, we have seen that there are open
subsets of
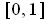 whose boundaries are not of measure zero. So even
constant functions on open sets might not be integrable. This is why we
need the next section.
whose boundaries are not of measure zero. So even
constant functions on open sets might not be integrable. This is why we
need the next section.
Extending the Integral: Partitions of Unity
The goal of this section is to define an integral for functions defined
on open sets. This is based on a technical result:
Theorem 3: (Partitions of Unity) Let
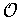 be an open cover
of a subset
be an open cover
of a subset
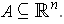 There is a set
There is a set
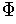 of
of
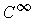 function
function
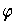 defined in an open set containing
defined in an open set containing
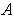 and satifying:
and satifying:
- For each
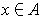 , one has
, one has
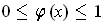 and
and
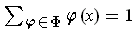 where the sum is defined because
for every such
where the sum is defined because
for every such
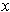 there is an open set
there is an open set
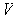 containing
containing
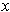 where there
are but finitely many
where there
are but finitely many
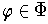 such that
such that
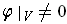 .
.
- For each
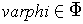 , there is a
, there is a
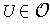 such that
such that
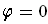 outside of some compact set contained in
outside of some compact set contained in
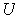 .
.
Definition 7: A set
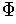 of functions satisfying condition (1)
of Theorem 3 is called a
of functions satisfying condition (1)
of Theorem 3 is called a
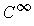 partition of unity of
partition of unity of
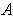 . When
both conditions are satisfied, we call
. When
both conditions are satisfied, we call
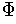 a partition of unity of
a partition of unity of
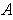 subordinate to the cover
subordinate to the cover
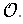
Lemma 1: (i) If
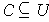 is a compact subset of an open set
is a compact subset of an open set
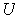 . Then there is a compact subset
. Then there is a compact subset
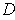 of
of
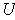 such that
such that
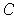 is contained in the
interior of
is contained in the
interior of
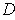 .
.
(ii) If
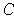 is a compact subset of an open set
is a compact subset of an open set
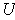 , then there is a
, then there is a
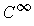 function
function
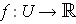 such that
such that
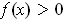 on all of
on all of
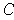 and such
and such
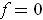 outside of a compact subset of
outside of a compact subset of
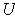 . In fact,
. In fact,
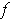 can
be chosen so it maps into
can
be chosen so it maps into
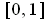 and such that
and such that
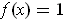 for all
for all
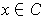 .
.
Proof: This is just Exercises 1-22 and 2-26.
Proof: (of Theorem 3) Case 1: First, consider the case in which
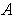 is compact.
Replace
is compact.
Replace
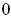 with a finite subcover of
with a finite subcover of
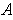 , say
, say
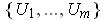 .
.
Claim: There are compact sets
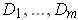 whose interiors cover
whose interiors cover
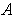 and such that
and such that
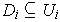 for every
for every
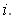
Proof: We make an inductive definition. Suppose, we have
already chosen
 such that the union of the their interiors and
the sets
such that the union of the their interiors and
the sets
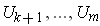 contains
contains
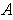 . Let
. Let
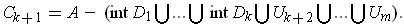
Then
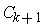 is a compact subset of
is a compact subset of
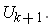 By Lemma 1 (i), there
is a compact set
By Lemma 1 (i), there
is a compact set
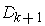 contained in
contained in
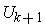 and containing
and containing
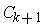 in
its interior. This completes the induction.
in
its interior. This completes the induction.
By Lemma 1 (ii), there are
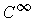 functions
functions
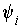 which are
positive on
which are
positive on
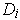 and which are zero outside of some compact subset of
and which are zero outside of some compact subset of
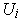 .
Then
.
Then
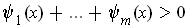 for
for
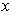 in an open set
in an open set
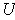 containing
containing
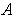 . Define functions
. Define functions
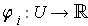 by
by
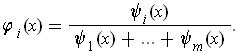
Now, choose a
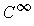 function
function
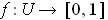 such that
such that
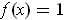 for
for
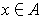 and such that
and such that
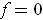 outside of a compact set contained in
outside of a compact set contained in
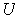 . Then the functions
. Then the functions
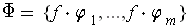 is the desired partition
of unity.
is the desired partition
of unity.
Case 2: Now, let's prove the result in case
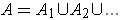 where
each
where
each
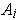 is compact and contained in the interior of
is compact and contained in the interior of
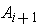 . To see
this, note that the compact set
. To see
this, note that the compact set
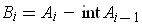 has an open cover
has an open cover
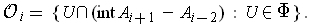 So, our previous case shows that there is a partition of unity
So, our previous case shows that there is a partition of unity
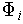 for
for
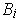 subordinate to
subordinate to
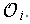 Now
Now
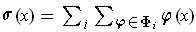 is a finite sum in some open set containing
is a finite sum in some open set containing
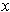 and so we can take as our
partition of unity the set of all the
and so we can take as our
partition of unity the set of all the
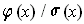 for all
for all
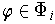 for all
for all
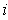 .
.
Case 3: Suppose now that
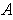 is an open set. This case follows
from the previous one by letting
is an open set. This case follows
from the previous one by letting
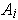 be the set of
be the set of
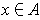 such that
such that
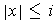 and the distance from
and the distance from
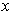 to the boundary of
to the boundary of
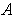 is at least
is at least
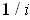 . The general case is now evident; one can simply replace the set
. The general case is now evident; one can simply replace the set
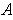 with the union of all the open subsets
with the union of all the open subsets
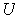 in
in
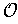 .
.
Definition 8: An open cover
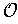 of a set
of a set
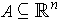 is called admissible if each element of
is called admissible if each element of
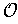 is contained in
is contained in
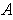 . Let
. Let
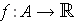 be a function and
be a function and
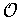 be admissible for
be admissible for
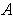 (and so
(and so
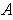 is open). Then
is open). Then
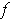 is said to be
integrable in the extended sense with integral
is said to be
integrable in the extended sense with integral
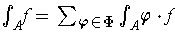 provided that the terms of
the series are defined and
provided that the terms of
the series are defined and
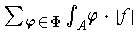 is convergent.
is convergent.
Theorem 4: Let
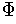 be a partition of unity subordinate to an
admissible cover
be a partition of unity subordinate to an
admissible cover
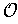 of an
open set
of an
open set
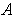 and
and
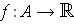 be a function integrable in the
extended sense (as defined using this this particular
be a function integrable in the
extended sense (as defined using this this particular
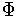 ).
).
- If
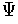 is another partition of unity subordinate to an admissible
cover
is another partition of unity subordinate to an admissible
cover
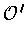 of
of
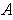 , then
, then
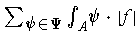 is convergent and
is convergent and
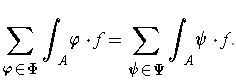
- If
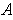 and
and
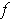 are bounded and the set of discontinuities of
are bounded and the set of discontinuities of
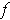 is a set of measure zero, then
is a set of measure zero, then
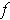 is integrable in the extended sense.
is integrable in the extended sense.
- If
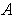 is Jordan-measurable and
is Jordan-measurable and
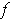 is bounded, then the extended
definition of
is bounded, then the extended
definition of
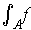 agrees with the earlier definition of
agrees with the earlier definition of
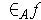 .
.
Proof: (i) For
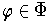 ,
,
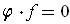 except on
a compact set
except on
a compact set
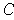 dependent on
dependent on
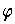 . For each
. For each
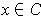 , there is an
open set containing
, there is an
open set containing
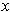 on which there are at most finitely many
on which there are at most finitely many
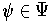 which are non-zero at some point in the open set. These open sets cover
which are non-zero at some point in the open set. These open sets cover
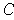 and so there is a finite subcover; hence there are only finitely many
and so there is a finite subcover; hence there are only finitely many
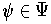 whose restrictions to
whose restrictions to
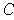 are not identically zero. One has
are not identically zero. One has
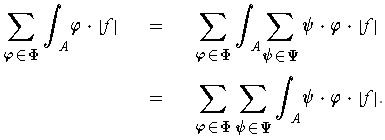
In particular, the right hand side converges. Absolute convergence implies
that we can re-arrange the series on the right as
A similar argument shows
that the same identities hold when the absolute values are removed.
(ii) Suppose
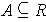 for some closed rectangle
for some closed rectangle
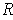 and that
and that
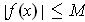 for some
for some
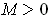 and all
and all
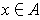 . Then for any finite
subset
. Then for any finite
subset
 , one has
, one has
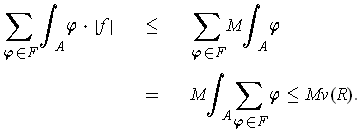
(iii) If
 is Jordan-measurable and
is Jordan-measurable and
 , then there is
a compact Jordan-measurable set
, then there is
a compact Jordan-measurable set
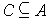 such that
such that
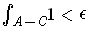 .
For any finite set
.
For any finite set
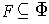 containing all the
containing all the
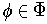 which
are not identically zero on
which
are not identically zero on
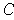 , one has:
, one has:
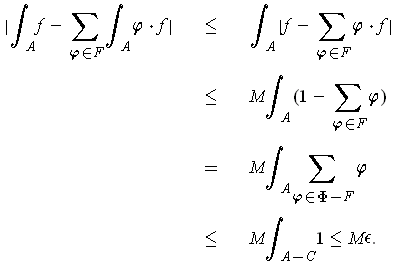
 is a sequence
is a sequence
 where
where
 .
A partition of a rectangle
.
A partition of a rectangle
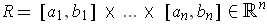 is an n-tuple
is an n-tuple
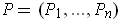 where
where
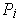 is a partition of
is a partition of
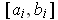 for every
for every
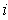 . A second partition
. A second partition
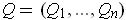 of the same rectangle is
called a refinement of the first partition
of the same rectangle is
called a refinement of the first partition
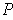 if the set
if the set
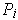 is a subset
of the set
is a subset
of the set
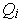 for each
for each
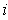 .
.
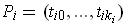 for each
for each
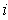 , then the partition P defines
the set of subrectangles of the partition
, then the partition P defines
the set of subrectangles of the partition
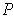 made up of all the
rectangles of the form
made up of all the
rectangles of the form
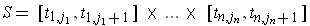 .
The volume
.
The volume
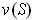 of the rectangle
of the rectangle
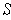 is defined to be
is defined to be
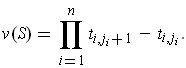
 is a bounded function defined
on the rectangle
is a bounded function defined
on the rectangle
 , then one defines for each subrectangle of
, then one defines for each subrectangle of
 the functions:
the functions:
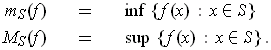
 for the partition
for the partition
 are defined to be
are defined to be
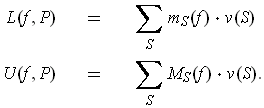
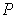 is a union of finitely many subrectangles of
is a union of finitely many subrectangles of
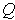 whose interiors are
pairwise disjoint. As a result, one has:
whose interiors are
pairwise disjoint. As a result, one has:
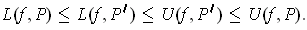
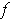 on
on
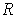 is defined
to be
is defined
to be
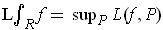 (respectively
(respectively
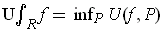 ). If
). If
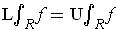 ,
then
,
then
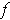 is called integrable with integral
is called integrable with integral
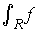 equal to this
common value. Another notation for the integral is
equal to this
common value. Another notation for the integral is
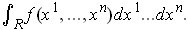
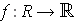 defined on
a rectangle
defined on
a rectangle
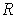 is integrable if and only if for every
is integrable if and only if for every
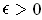 ,
there is a partition
,
there is a partition
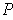 such that
such that
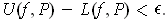
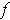 is integrable and
is integrable and
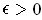 , then there are partitions
, then there are partitions
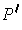 and
and
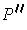 such that
such that
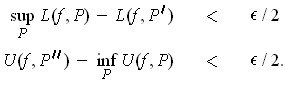
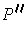 be a refinement of both
be a refinement of both
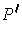 and
and
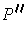 . Then Lemma 1 implies that
. Then Lemma 1 implies that
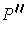 is a partition of the desired type.
is a partition of the desired type.
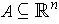 and
and
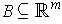 be closed rectangles and
be closed rectangles and
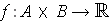 be integrable. For
be integrable. For
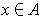 , let
, let
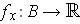 be defined by
be defined by
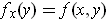 and let
and let
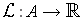 and
and
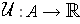 be defined by:
be defined by:
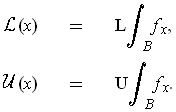
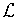 and
and
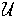 are both integrable on
are both integrable on
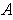 and
and
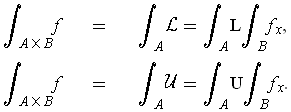
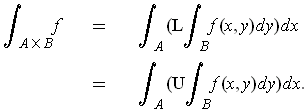
 (respectively
(respectively
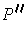 ) is a partition of
) is a partition of
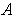 (respectively
(respectively
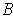 ), then
), then
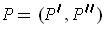 is a partition of
is a partition of
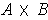 with subrectangles of the
form
with subrectangles of the
form
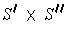 where
where
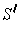 is a subrectangle of
is a subrectangle of
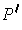 and
and
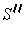 is a
subrectangle of
is a
subrectangle of
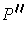 .
.
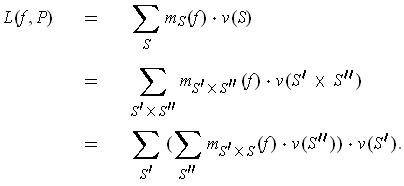
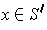 , one has
, one has
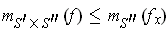 , and so
, and so
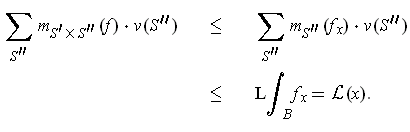
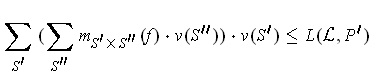
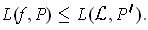
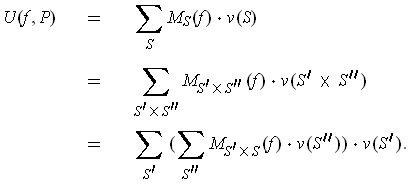
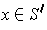 , one has
, one has
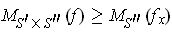 , and so
, and so
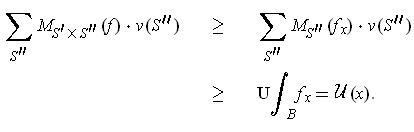
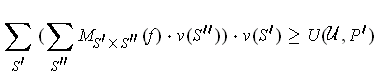
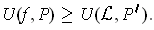
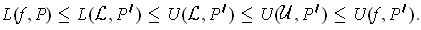
 is integrable,
is integrable,
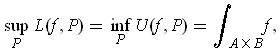
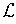 is integrable with integral equal to
is integrable with integral equal to
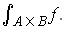
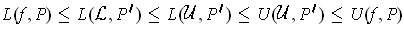
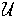 is integrable with integral
is integrable with integral
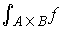 ,
as desired.
,
as desired.
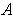 and
and
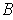 , one can show that
the order in which the integrals are iterated does not affect the result.
, one can show that
the order in which the integrals are iterated does not affect the result.
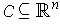 , then its characteristic
function
, then its characteristic
function
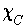 is defined by
is defined by
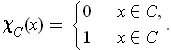
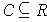 where
where
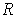 is a closed rectangle, then a bounded function
is a closed rectangle, then a bounded function
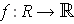 is said to be integrable with integral
is said to be integrable with integral
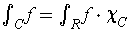 provided that this last quantity is defined.
provided that this last quantity is defined.
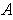 of
of
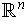 is said to be of
measure zero (respectively content zero) if for every
is said to be of
measure zero (respectively content zero) if for every
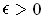 ,
there is a countable infinite (respectively finite) sequence
,
there is a countable infinite (respectively finite) sequence
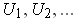 of open rectangles which form a cover of
of open rectangles which form a cover of
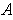 and such that
and such that
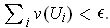
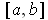 with
with
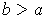 is not of measure zero.
is not of measure zero.
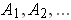 is a countable sequence of
sets of measure zero and
is a countable sequence of
sets of measure zero and
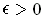 . Then
. Then
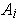 has an open cover by
rectangles
has an open cover by
rectangles
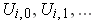 such that
such that
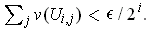 Then clearly the
Then clearly the
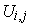 are a cover of the union of
are a cover of the union of
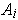 and the sum of
their volumes is less than
and the sum of
their volumes is less than
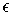 (why?). To enumerate the
(why?). To enumerate the
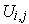 , just
list them out in order of increasing
, just
list them out in order of increasing
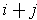 keeping those with the same value of
keeping those with the same value of
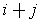 in order of increasing
in order of increasing
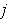 .
.
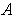 is compact and of measure 0, with an open covering
is compact and of measure 0, with an open covering
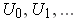 of open
rectangles of total volume less than
of open
rectangles of total volume less than
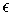 . Then any finite subcover
satisfies the same condition. So
. Then any finite subcover
satisfies the same condition. So
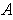 is also of content zero.
is also of content zero.
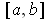 were of measure zero, it would be of content zero by
part (ii). Suppose
were of measure zero, it would be of content zero by
part (ii). Suppose
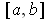 has a cover
has a cover
 by closed rectangles of
total length less than
by closed rectangles of
total length less than
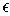 . We can replace the
. We can replace the
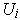 with their
intersections with
with their
intersections with
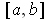 to show that the
to show that the
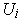 can be assumed to be
subintervals of
can be assumed to be
subintervals of
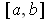 . But then the endpoints of the
. But then the endpoints of the
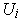 can be arranged
into increasing order to obtain a partition of
can be arranged
into increasing order to obtain a partition of
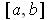 . Each
. Each
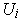 is
a union of certain of the subrectangles of this partition and so
is
a union of certain of the subrectangles of this partition and so
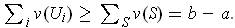 So, if
So, if
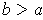 , the interval
, the interval
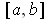 cannot be of content zero and so it is also not of measure zero.
cannot be of content zero and so it is also not of measure zero.
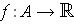 be a bounded function and
be a bounded function and
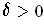 .
Define the functions:
.
Define the functions:
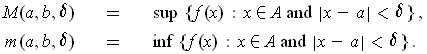
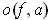 of
of
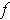 at
at
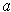 is defined to be
is defined to be
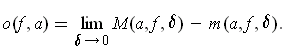
 is continuous at
is continuous at
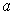 if
and only if
if
and only if
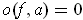 .
.
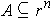 is closed,
is closed,
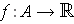 is
bounded, and
is
bounded, and
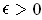 , then
, then
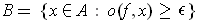 is closed.
is closed.
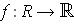 is a bounded function defined on a closed
rectangle
is a bounded function defined on a closed
rectangle
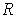 and
and
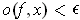 for some
for some
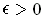 , then
there is a partition
, then
there is a partition
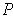 of
of
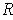 such that
such that
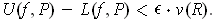
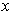 is not in
is not in
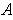 , then there is an open an open ball of radius
, then there is an open an open ball of radius
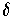 about
about
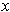 which is disjoint from
which is disjoint from
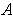 . Using this ball, one can check that
. Using this ball, one can check that
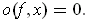 So
So
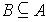 .
.
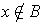 and
and
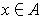 . Then
. Then
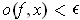 . Choose a
. Choose a
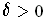 such that
such that
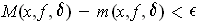 . Then for all
. Then for all
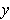 such that
such that
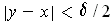 , we have
, we have
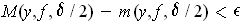 .
and so
.
and so
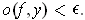 . Thus the complement of
. Thus the complement of
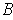 is open and
is open and
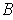 is
closed.
is
closed.
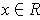 there is a closed rectangle with
there is a closed rectangle with
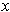 in its interior
such that
in its interior
such that
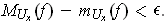 Since
Since
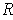 is compact, a
finite number of these are such that their interiors cover
is compact, a
finite number of these are such that their interiors cover
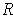 . Choose for
. Choose for
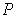 any partition of
any partition of
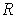 such that every subrectangle
such that every subrectangle
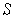 of
of
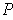 is contained in one
of these finitely many
is contained in one
of these finitely many
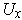 's. Then
's. Then
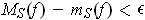 for each
subrectangle
for each
subrectangle
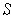 . It follows that
. It follows that
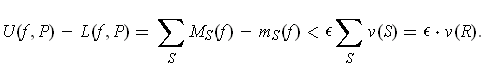
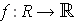 be a bounded function defined
on a closed rectangle
be a bounded function defined
on a closed rectangle
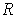 and let
and let
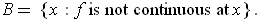 Then
Then
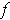 is integrable if and only if
is integrable if and only if
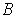 is a set of measure zero.
is a set of measure zero.
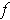 is integrable and
is integrable and
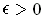 . For
. For
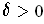 ,
choose a partition
,
choose a partition
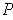 of
of
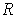 such that
such that
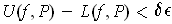 .
Then the set of subrectangles
.
Then the set of subrectangles
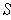 of
of
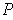 such that
such that
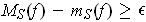 has total volume less than
has total volume less than
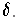 If
If
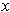 is a point where the oscillation of
is a point where the oscillation of
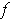 is
at least
is
at least
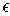 and if
and if
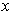 is in the interior of one of the subrectangles
of
is in the interior of one of the subrectangles
of
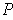 , then
, then
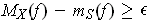 . Since the boundaries of the
subrectangles of
. Since the boundaries of the
subrectangles of
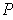 is a set of measure zero, it follows that the set
is a set of measure zero, it follows that the set
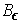 of
of
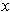 with
oscillation at least
with
oscillation at least
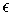 must be a set of content (and hence measure) zero.
Since the set of discontuities of the function
must be a set of content (and hence measure) zero.
Since the set of discontuities of the function
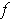 is just the union of the
countably many sets
is just the union of the
countably many sets
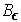 for
for
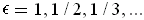 , it follows
that the set of discontinuities of
, it follows
that the set of discontinuities of
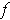 is also of measure zero.
is also of measure zero.
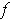 is of measure 0.
As before, let
is of measure 0.
As before, let
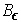 be the set of
be the set of
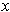 satisfying
satisfying
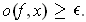 Since
Since
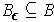 is compact by Proposition 3 and
is compact by Proposition 3 and
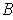 is of
measure zero,
is of
measure zero,
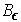 is of content zero. In particular, there is
a finite set of closed rectangles whose interiors cover
is of content zero. In particular, there is
a finite set of closed rectangles whose interiors cover
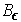 and such that their
total volume is at most
and such that their
total volume is at most
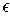 . First choose a partition
. First choose a partition
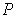 of
of
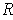 such
that every subrectangle of
such
that every subrectangle of
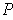 is either completely contained with one of
the finitely many rectangles or else its interior is disjoint from all of these
rectangles. For each rectangle of the first type, one has
is either completely contained with one of
the finitely many rectangles or else its interior is disjoint from all of these
rectangles. For each rectangle of the first type, one has
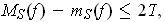 where
where
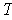 is an upper bound for |f(x)| for all
is an upper bound for |f(x)| for all
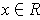 .
For each subrectangle S of the second type, one can use Proposition 3(iii)
to find a partition of the subrectangle such that the difference between
the upper and lower sums on this subrectangle is at most
.
For each subrectangle S of the second type, one can use Proposition 3(iii)
to find a partition of the subrectangle such that the difference between
the upper and lower sums on this subrectangle is at most
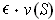 .
Now replace P with a refinement of each of these partitions. Then we
have
.
Now replace P with a refinement of each of these partitions. Then we
have
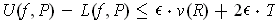 .
By making
.
By making
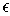 sufficiently small, we can make this sum as small as we like, and so
sufficiently small, we can make this sum as small as we like, and so
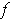 is integrable.
is integrable.
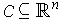 be a bounded set. Then
its characteristic function
be a bounded set. Then
its characteristic function
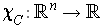 is
integrable if and only if the boundary of
is
integrable if and only if the boundary of
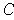 is of measure zero.
is of measure zero.
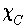 is precisely the boundary of
is precisely the boundary of
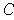 .
.
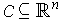 is called
Jordan measurable if its boundary is of measure zero. In this
case, the integral of its characteristic function is called
the content of
is called
Jordan measurable if its boundary is of measure zero. In this
case, the integral of its characteristic function is called
the content of
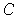 or its (n-dimensional) volume.
or its (n-dimensional) volume.
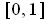 whose boundaries are not of measure zero. So even
constant functions on open sets might not be integrable. This is why we
need the next section.
whose boundaries are not of measure zero. So even
constant functions on open sets might not be integrable. This is why we
need the next section.
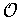 be an open cover
of a subset
be an open cover
of a subset
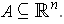 There is a set
There is a set
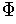 of
of
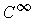 function
function
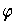 defined in an open set containing
defined in an open set containing
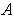 and satifying:
and satifying:
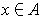 , one has
, one has
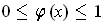 and
and
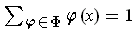 where the sum is defined because
for every such
where the sum is defined because
for every such
 there is an open set
there is an open set
 containing
containing
 where there
are but finitely many
where there
are but finitely many
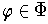 such that
such that
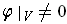 .
.
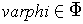 , there is a
, there is a
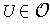 such that
such that
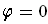 outside of some compact set contained in
outside of some compact set contained in
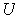 .
.
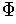 of functions satisfying condition (1)
of Theorem 3 is called a
of functions satisfying condition (1)
of Theorem 3 is called a
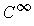 partition of unity of
partition of unity of
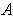 . When
both conditions are satisfied, we call
. When
both conditions are satisfied, we call
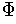 a partition of unity of
a partition of unity of
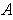 subordinate to the cover
subordinate to the cover
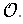
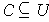 is a compact subset of an open set
is a compact subset of an open set
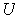 . Then there is a compact subset
. Then there is a compact subset
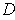 of
of
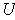 such that
such that
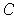 is contained in the
interior of
is contained in the
interior of
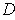 .
.
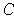 is a compact subset of an open set
is a compact subset of an open set
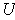 , then there is a
, then there is a
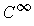 function
function
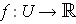 such that
such that
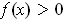 on all of
on all of
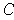 and such
and such
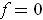 outside of a compact subset of
outside of a compact subset of
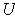 . In fact,
. In fact,
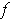 can
be chosen so it maps into
can
be chosen so it maps into
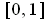 and such that
and such that
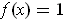 for all
for all
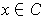 .
.
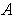 is compact.
Replace
is compact.
Replace
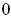 with a finite subcover of
with a finite subcover of
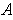 , say
, say
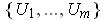 .
.
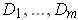 whose interiors cover
whose interiors cover
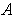 and such that
and such that
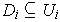 for every
for every
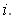
 such that the union of the their interiors and
the sets
such that the union of the their interiors and
the sets
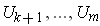 contains
contains
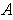 . Let
. Let
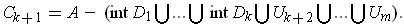
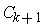 is a compact subset of
is a compact subset of
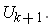 By Lemma 1 (i), there
is a compact set
By Lemma 1 (i), there
is a compact set
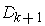 contained in
contained in
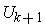 and containing
and containing
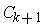 in
its interior. This completes the induction.
in
its interior. This completes the induction.
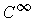 functions
functions
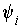 which are
positive on
which are
positive on
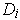 and which are zero outside of some compact subset of
and which are zero outside of some compact subset of
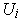 .
Then
.
Then
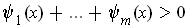 for
for
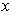 in an open set
in an open set
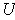 containing
containing
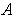 . Define functions
. Define functions
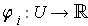 by
by
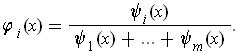
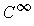 function
function
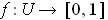 such that
such that
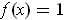 for
for
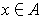 and such that
and such that
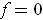 outside of a compact set contained in
outside of a compact set contained in
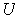 . Then the functions
. Then the functions
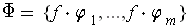 is the desired partition
of unity.
is the desired partition
of unity.
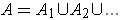 where
each
where
each
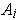 is compact and contained in the interior of
is compact and contained in the interior of
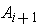 . To see
this, note that the compact set
. To see
this, note that the compact set
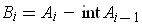 has an open cover
has an open cover
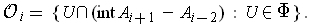 So, our previous case shows that there is a partition of unity
So, our previous case shows that there is a partition of unity
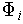 for
for
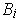 subordinate to
subordinate to
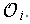 Now
Now
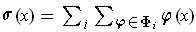 is a finite sum in some open set containing
is a finite sum in some open set containing
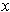 and so we can take as our
partition of unity the set of all the
and so we can take as our
partition of unity the set of all the
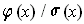 for all
for all
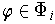 for all
for all
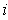 .
.
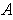 is an open set. This case follows
from the previous one by letting
is an open set. This case follows
from the previous one by letting
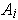 be the set of
be the set of
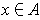 such that
such that
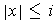 and the distance from
and the distance from
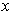 to the boundary of
to the boundary of
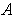 is at least
is at least
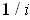 . The general case is now evident; one can simply replace the set
. The general case is now evident; one can simply replace the set
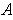 with the union of all the open subsets
with the union of all the open subsets
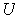 in
in
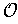 .
.
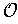 of a set
of a set
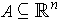 is called admissible if each element of
is called admissible if each element of
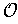 is contained in
is contained in
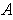 . Let
. Let
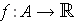 be a function and
be a function and
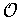 be admissible for
be admissible for
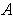 (and so
(and so
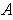 is open). Then
is open). Then
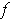 is said to be
integrable in the extended sense with integral
is said to be
integrable in the extended sense with integral
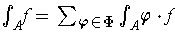 provided that the terms of
the series are defined and
provided that the terms of
the series are defined and
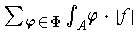 is convergent.
is convergent.
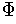 be a partition of unity subordinate to an
admissible cover
be a partition of unity subordinate to an
admissible cover
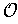 of an
open set
of an
open set
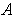 and
and
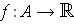 be a function integrable in the
extended sense (as defined using this this particular
be a function integrable in the
extended sense (as defined using this this particular
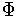 ).
).
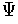 is another partition of unity subordinate to an admissible
cover
is another partition of unity subordinate to an admissible
cover
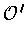 of
of
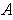 , then
, then
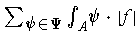 is convergent and
is convergent and
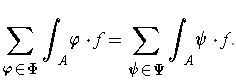
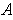 and
and
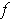 are bounded and the set of discontinuities of
are bounded and the set of discontinuities of
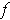 is a set of measure zero, then
is a set of measure zero, then
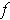 is integrable in the extended sense.
is integrable in the extended sense.
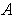 is Jordan-measurable and
is Jordan-measurable and
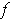 is bounded, then the extended
definition of
is bounded, then the extended
definition of
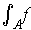 agrees with the earlier definition of
agrees with the earlier definition of
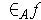 .
.
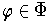 ,
,
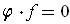 except on
a compact set
except on
a compact set
 dependent on
dependent on
 . For each
. For each
 , there is an
open set containing
, there is an
open set containing
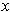 on which there are at most finitely many
on which there are at most finitely many
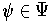 which are non-zero at some point in the open set. These open sets cover
which are non-zero at some point in the open set. These open sets cover
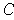 and so there is a finite subcover; hence there are only finitely many
and so there is a finite subcover; hence there are only finitely many
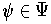 whose restrictions to
whose restrictions to
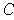 are not identically zero. One has
are not identically zero. One has
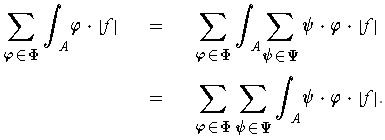
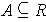 for some closed rectangle
for some closed rectangle
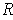 and that
and that
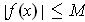 for some
for some
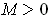 and all
and all
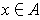 . Then for any finite
subset
. Then for any finite
subset
 , one has
, one has
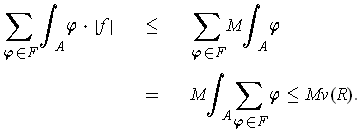
 is Jordan-measurable and
is Jordan-measurable and
 , then there is
a compact Jordan-measurable set
, then there is
a compact Jordan-measurable set
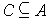 such that
such that
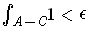 .
For any finite set
.
For any finite set
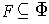 containing all the
containing all the
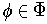 which
are not identically zero on
which
are not identically zero on
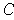 , one has:
, one has: