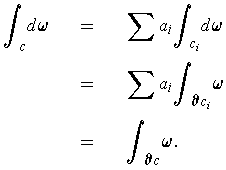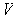 be a vector space over
be a vector space over
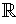 . A function
. A function
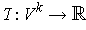 is said to be k-multilinear (or to be a k-tensor
) if and only if it is linear in each of its k variables. The set of
all k-tensors over
is said to be k-multilinear (or to be a k-tensor
) if and only if it is linear in each of its k variables. The set of
all k-tensors over
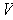 is denoted
is denoted
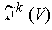 .
.
This section is concerned with some algebraic preliminaries needed to give a formal definition of what we mean by a differenial form.
Definition 1: Let
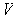 be a vector space over
be a vector space over
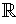 . A function
. A function
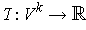 is said to be k-multilinear (or to be a k-tensor
) if and only if it is linear in each of its k variables. The set of
all k-tensors over
is said to be k-multilinear (or to be a k-tensor
) if and only if it is linear in each of its k variables. The set of
all k-tensors over
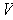 is denoted
is denoted
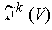 .
.
Note:
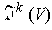 with the obvious operations is a vector
space over
with the obvious operations is a vector
space over
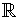 . One can define the tensor product function
. One can define the tensor product function
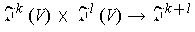 by
by
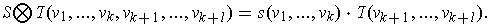
This is clearly a bilinear map, and the tensor product is associative.
Proposition 1: The vector space
 is of dimension
is of dimension
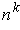 where
where
 is the dimension of
is the dimension of
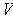 . In particular, if
. In particular, if
 is a basis of
is a basis of
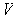 , and
, and
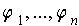 is the corresponding dual
basis, then the
is the corresponding dual
basis, then the
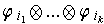 form a basis
of
form a basis
of
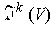 .
.
Proof: Clearly the tensor products are elements of
 .
If
.
If
 is a k-tensor, then it is easy to verify that
is a k-tensor, then it is easy to verify that
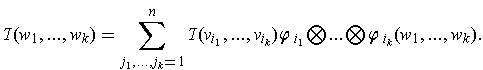
Finally, if
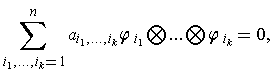
then evaluating the left side at
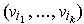 shows that
shows that
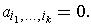
Definition 2: A k-tensor
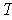 over
over
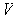 is said to alternating
if interchanging any two of its variables changes the sign of the functional
value, i.e.
is said to alternating
if interchanging any two of its variables changes the sign of the functional
value, i.e.
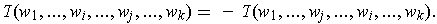
The set of alternating k-tensors over
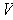 is denoted
is denoted
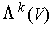 .
.
Note: Clearly,
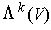 is a vector subspace of
is a vector subspace of
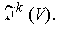 For any k-tensor
For any k-tensor
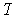 , one could make a symmetric k-tensor
, one could make a symmetric k-tensor
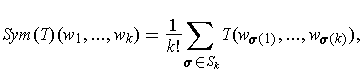
where
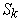 is the set of all permutations of
is the set of all permutations of
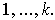 If we let
If we let
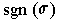 denote the sign of the permutation
denote the sign of the permutation
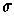 (i.e. it is 1 or -1 depending on
whether the permutation is a product of an even or odd number of transpositions), then
it is not surprising that
(i.e. it is 1 or -1 depending on
whether the permutation is a product of an even or odd number of transpositions), then
it is not surprising that
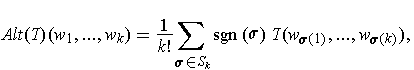
should be alternating. In fact, one has:
Proposition 2:
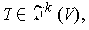 then
then
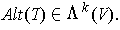
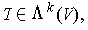 then
then
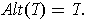
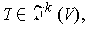 then
then
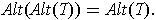
Proof: This is a straightforward consequence of the definitions.
Definition 3: The wedge product is the map
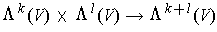 defined by
defined by
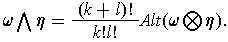
For any linear map
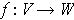 , there is a natural map
, there is a natural map
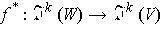 defined by
defined by
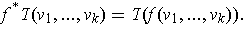 Restricting this
to alternating k-tensors gives another map (also denoted by the same symbol)
Restricting this
to alternating k-tensors gives another map (also denoted by the same symbol)
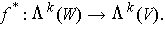 The following is an easy exercise:
The following is an easy exercise:
Proposition 3: The wedge product is a bilinear map satisfying
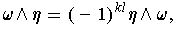
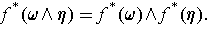
The wedge product is also associative:
Proposition 4:
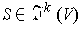 and
and
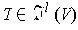 , then
, then
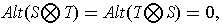
provided that


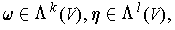 , and
, and
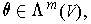 then
then
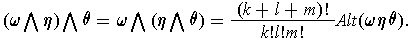
Proof: Let
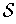 be the group of all permutations on
be the group of all permutations on
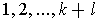 and
and
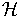 be the subgroup of permutations which fix
be the subgroup of permutations which fix
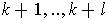 . Then
the cosets of
. Then
the cosets of
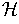 in
in
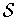 are mutually disjoint and so one can write
are mutually disjoint and so one can write
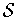 as a disjoint
union
as a disjoint
union
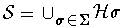 for a certain set
for a certain set
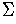 of elements of
of elements of
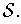 One has
One has
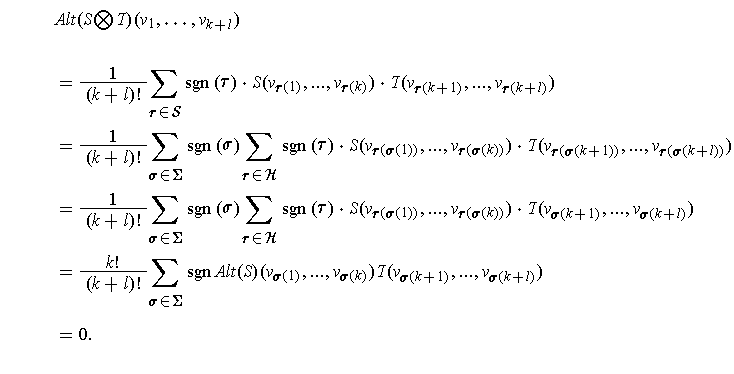
For the second assertion, apply the first result with
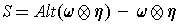 and
and
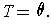 The fact that
The fact that
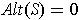 follows from the fact that
follows from the fact that
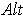 is idempotent. Similarly, one can apply the first result with
is idempotent. Similarly, one can apply the first result with
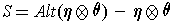 and
and
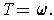
The final assertion follows from the second and the definition of the wedge product.
Proposition 5: The vector space
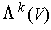 is of dimension
is of dimension
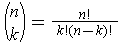 where
where
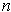 is the dimension
of the vector space
is the dimension
of the vector space
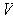 . In particular, if
. In particular, if
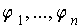 is
a dual basis, then the
is
a dual basis, then the
 where
where
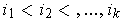 form a basis for
form a basis for
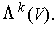
Proof: To show that the set spans
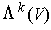 , apply
, apply
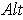 to
an expression for the alternating k-tensor in terms of the basis
of Proposition 1. The linear independense is shown analogously to the
argument of Proposition 1.
to
an expression for the alternating k-tensor in terms of the basis
of Proposition 1. The linear independense is shown analogously to the
argument of Proposition 1.
Proposition 6: Let
 be a basis of the vector space
be a basis of the vector space
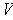 and
and
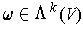 . If
. If
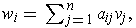 then
then
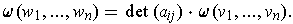
Proof: Proposition 5 says that
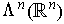 is of
dimension 1, and the determinant function is the a non-zero alternating
n-tensor. But
is of
dimension 1, and the determinant function is the a non-zero alternating
n-tensor. But
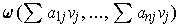 can be thought
of as an alternating n-tensor on
can be thought
of as an alternating n-tensor on
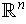 . So it is a constant
multiple of
. So it is a constant
multiple of
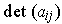 . Substituting
. Substituting
 , shows that
the constant must be
, shows that
the constant must be
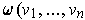 .
.
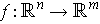 can be viewed as a function
which assigns to each point in
can be viewed as a function
which assigns to each point in
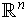 a vector in
a vector in
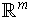 .
There are several possible interpretations of the target space. Here
are two:
.
There are several possible interpretations of the target space. Here
are two:
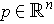 , has a tangent space whose
elements are of the form
, has a tangent space whose
elements are of the form
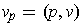 where
where
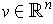 . So the
map
. So the
map
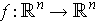 can be viewed as assigning to
each point an vector in its tangent space. When we view
can be viewed as assigning to
each point an vector in its tangent space. When we view
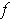 in this
way, we call it a vector field.
in this
way, we call it a vector field.
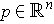 , we can associate a copy
, we can associate a copy
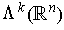 denoted
denoted
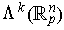 whose elements are alternating k-tensors
in the tangent space at
whose elements are alternating k-tensors
in the tangent space at
 . When we view the function
. When we view the function
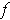 as mapping
points to alternating k-tensors of the tangent space at
as mapping
points to alternating k-tensors of the tangent space at
 , we call
, we call
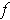 a k-form (or differential form) on
a k-form (or differential form) on
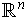 .
.
In both cases we can express the vectors in terms of a standard basis,
and so we have a certain number of coodinate functions. When these
coordinate functions are continuous, differential, etc., we call the
vector field or k-form continuous, differentiable, etc. To simplify the
hypotheses, we will henceforth use the word differentiable to
mean
 .
.
Definition 4: If
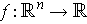 is differentiable,
the 1-form
is differentiable,
the 1-form
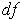 is defined by
is defined by
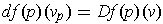
for
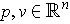 . In the special case of the projection
. In the special case of the projection
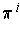 , one
denotes
, one
denotes
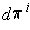 as
as
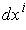 .
.
Note:
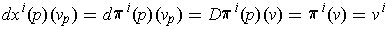 and
so
and
so
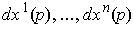 is the dual basis to
is the dual basis to
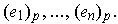 In
particular, we will usually write k-forms as
In
particular, we will usually write k-forms as
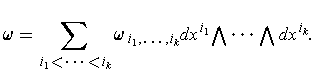
An immediate consequence of this notation is:
Proposition 7: If
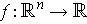 is differentiable,
then
is differentiable,
then
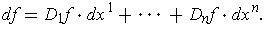
The next definition tells us how to do substitutions in k-forms:
Definition 5: Let
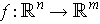 is a differentiable
function and
is a differentiable
function and
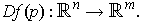 be the linear transformation
defined by its derivative at
be the linear transformation
defined by its derivative at
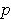 . This map can be viewed as mapping the
tangent spaces, i.e. we have a function
. This map can be viewed as mapping the
tangent spaces, i.e. we have a function
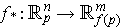 defined by
defined by
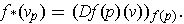
Now,
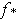 defines
defines
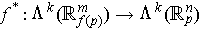 .
If
.
If
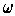 is a k-form on
is a k-form on
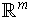 , then
, then
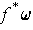 is the
k-form on
is the
k-form on
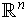 defined by
defined by
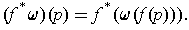
Note: To be more explicit, for
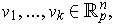 one
has
one
has
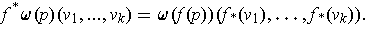
The next proposition tells us how to compute substitutions:
Proposition 8: If
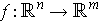 is differentiable,
then
is differentiable,
then
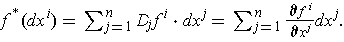
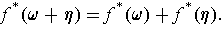
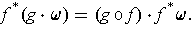
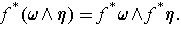
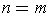 , then
, then
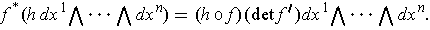
Proof: Should be here.
Definition 4 can be extended to higher order forms as follows:
Definition 6: Given a differentiable k-form
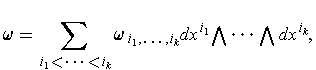
the differential of
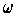 is the (k+1)-form defined by
is the (k+1)-form defined by
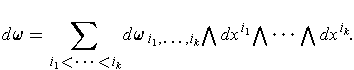
To calculate differentials of k_forms, one has:
Proposition 9:

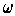 is a
is a
 -form and
-form and
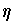 is an
is an
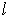 -form, then
-form, then
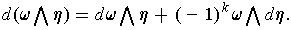
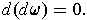
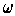 is a
is a
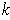 -form on
-form on
 and
and
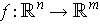 is differentiable, then
is differentiable, then

Proof: The first assertion is obvious from the definition, and the second asesertion follows from the formula for differentiating a product and assertion (1) of Proposition 3. The third assertion follows from assertion (1) of Proposition 3 and the equality of mixed partials:
This leaves the last assertion. The case of 0-forms is just the chain
rule. Assume that the assertion is true for all
 -forms
-forms
 ; then it
suffices to show it for
; then it
suffices to show it for
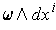 . One has
. One has
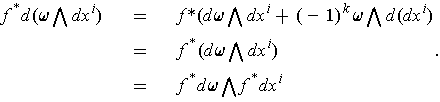
On the other hand,
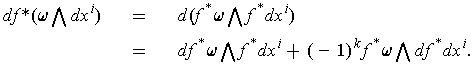
This proves the result since
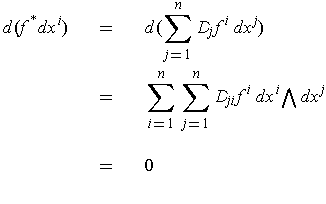
where we have used equality of mixed partials.
Definition 7: A singular n-cube in
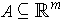 is a continuous function
is a continuous function
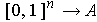 . The convention in case
. The convention in case
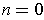 , is
that
, is
that
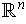 and
and
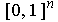 are both the set
are both the set
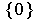 . A singular 1-cube
is called a curve. The standard n-cube is the inclusion map
of
. A singular 1-cube
is called a curve. The standard n-cube is the inclusion map
of
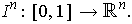 An n-chain a linear combination with integer
coefficients of singular n-cubes (i.e. an element of the free Abelian group
generated by the singular n-cubes).
An n-chain a linear combination with integer
coefficients of singular n-cubes (i.e. an element of the free Abelian group
generated by the singular n-cubes).
Given the standard n-cube
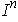 , for
, for
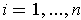 and
and
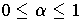 the
singular (n-1) cube
the
singular (n-1) cube
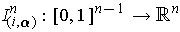 by
by
 where
where
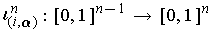 is defined by
is defined by
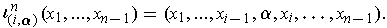 In the case where
In the case where
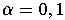 , the singular n-cube
, the singular n-cube
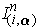 is
called the
is
called the
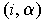 -face of
-face of
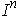 . The boundary
. The boundary
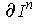 of
of
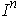 is defined by
is defined by
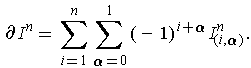
The
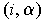 -face of a singular n-cube
-face of a singular n-cube
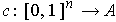 is
the composition
is
the composition
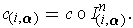 The boundary
of
The boundary
of
 is the (n-1)-chain
is the (n-1)-chain
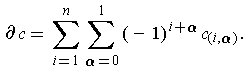
Finally, the boundary of an n-chain
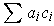 is defined to be the
(n-1)-chain
is defined to be the
(n-1)-chain

The signs have been set up to guarantee
Proposition 10: If
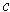 is an
is an
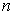 -chain in
-chain in
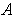 , then
, then
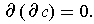
Proof: The proof is straightforward. The idea is that taking an
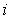 -face of a
-face of a
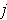 -face is the same as taking the
-face is the same as taking the
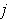 -face of an
-face of an
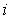 -face. So,
it is just a matter of checking that the signs come out right.
-face. So,
it is just a matter of checking that the signs come out right.
We are now ready to define integrals of differential forms over chains:
Definition 8:
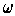 is a
is a
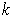 -form on
-form on
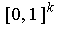 , then
, then
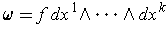 for some unique function
for some unique function
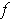 . Define
. Define
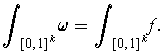
which can be written
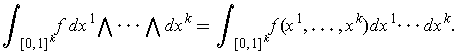
In the case of a 0-form, define the integral to be
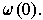
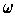 is a
is a
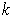 -form on
-form on
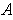 and
and
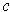 is a singular
is a singular
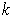 -cube in
-cube in
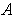 ,
define
,
define
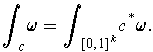
In the case of a 0-form, define the integral to be
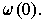
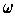 is a
is a
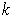 -form on
-form on
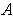 and
and
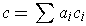 is a
is a
 -chain in
-chain in
 , define
, define
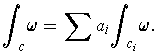
Note: In the special case of a standard
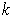 -cube
-cube
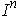 , the integral of
, the integral of
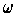 over
over
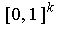 is equal to the integral of
is equal to the integral of
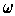 over the
over the
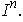 An integral of a 1-form (respectively 2-form) over a 1-chain (respectively
2-chain) is often referred to as a line integral (respectively
surface integral).
An integral of a 1-form (respectively 2-form) over a 1-chain (respectively
2-chain) is often referred to as a line integral (respectively
surface integral).
The main theorem of the course is:
Theorem 1: (Stokes' Theorem) If
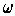 is a
is a
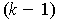 -form on an
open set
-form on an
open set
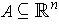 and
and
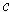 is a
is a
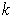 -chain in
-chain in
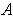 , then
, then
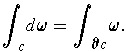
Proof: First consider the case where
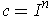 and
and
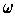 is
a
is
a
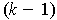 -form on
-form on
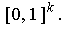 Using additivity, it is clearly enough to
consider the case where
Using additivity, it is clearly enough to
consider the case where
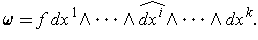
One has
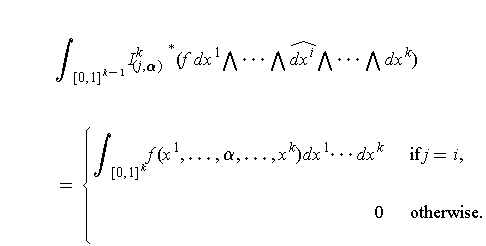
It follows that
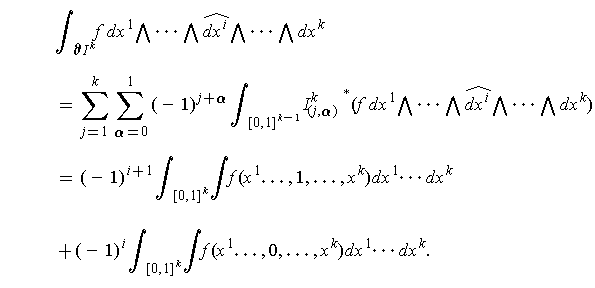
Considering the other side of the equation,
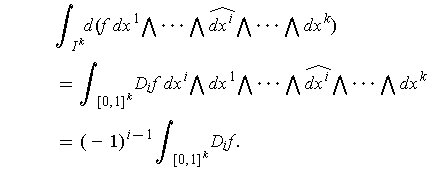
Using Fubini's Theorem and the one dimensional Fundamental Theorem of Calculus, to evaluate this:
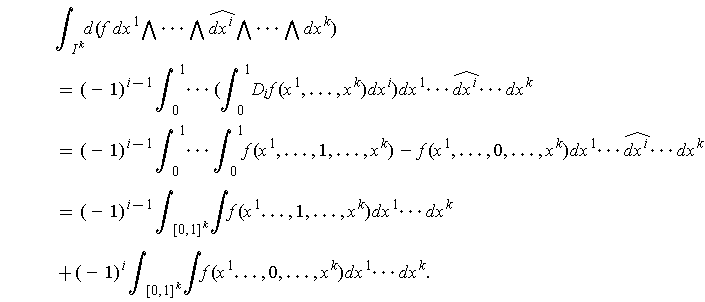
which is the same result as we had before. So the result holds in this case.
Now consider the case of a singular
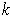 -cube
-cube
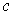 . One has by definition:
. One has by definition:
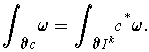
And so,
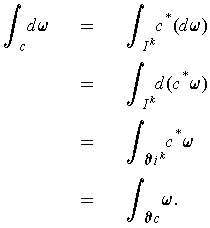
Finally, in the general case where
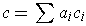 is a
is a
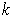 -chain, one has
-chain, one has