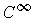 .
.
Throughout this lecture, the word differentiable will be used to
mean
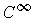 .
.
Definition 1: A diffeomorphism is a function
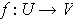 between open sets of
between open sets of
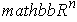 which is differentiable and has a
differentiable inverse.
which is differentiable and has a
differentiable inverse.
Definition 2: The half-space
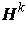 is the set of points in
is the set of points in
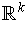 whose last coordinate is non-negative. A k-dimensional
manifold-with-boundary is a subset
whose last coordinate is non-negative. A k-dimensional
manifold-with-boundary is a subset
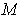 of
of
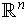 such that
every point
such that
every point
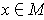 satisfies:
satisfies:
There is a diffeomorphism
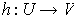 from an open neighborhood of
from an open neighborhood of
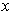 such that
such that
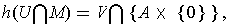
where the set
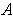 is either
is either
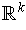 or
or
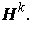
The set of
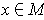 which satisfy the condition with
which satisfy the condition with
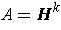 is called the boundary of
is called the boundary of
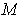 and is denoted
and is denoted
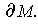 If the boundary of
If the boundary of
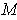 is empty, then
is empty, then
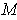 can be referred to as a
manifold.
can be referred to as a
manifold.
If
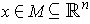 , then a coordinate system
around
, then a coordinate system
around
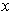 is a 1-1 differentiable function
is a 1-1 differentiable function
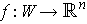 for
which there is an open set
for
which there is an open set
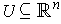 satisfying:
satisfying:
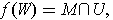
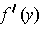 has rank
has rank
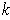 for each
for each
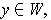
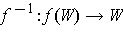 is continuous.
is continuous.
Proposition 1: A subset
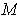 of
of
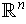 is a k-dimensional
manifold if and only if every
is a k-dimensional
manifold if and only if every
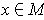 has a coordinate system about
has a coordinate system about
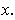
Proof: If
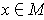 has a function
has a function
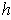 as in the definition of
manifold, then let
as in the definition of
manifold, then let
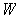 be the projection on the first
be the projection on the first
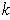 coordinates of
coordinates of
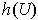 and
and
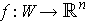 be defined by
be defined by
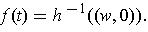 Then
Then
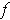 is a coordinate system about
is a coordinate system about
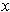 . (The condition involving the
rank follows by applying the chain rule to
. (The condition involving the
rank follows by applying the chain rule to
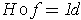 where
where
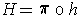 is
with
is
with
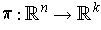 being the projection on the first
being the projection on the first
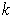 coordinates.)
coordinates.)
Conversely, if
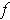 is a coordinate system about
is a coordinate system about
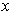 , then define
, then define
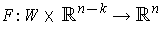 by
by
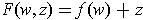 . If
. If
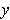 is such that
is such that
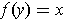 , then
, then
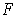 is invertible in a neighborhood of
is invertible in a neighborhood of
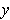 . The inverse in this neighborhood is the desired function
. The inverse in this neighborhood is the desired function
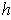 as in
the definition of manifold.
as in
the definition of manifold.
Note: If
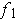 and
and
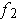 are a coordinate systems about
are a coordinate systems about
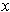 , then
, then
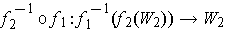 is a diffeomorphism as the
proof showed that
is a diffeomorphism as the
proof showed that
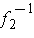 is just the first
is just the first
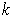 coordinates of the
diffeomorphism
coordinates of the
diffeomorphism
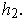
In particular,
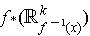 is independent of the
choice of coordinate system
is independent of the
choice of coordinate system
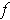 about
about
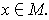 This set is called
the tangent space of
This set is called
the tangent space of
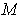 at
at
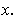 If
If
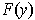 is a element of the
tangent space at
is a element of the
tangent space at
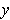 for every
for every
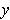 in
in
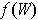 , then there is a unique
, then there is a unique
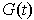 in the tangent space of
in the tangent space of
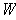 at
at
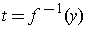 such that
such that
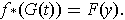 We say
We say
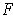 is a differentiable vector field of
is a differentiable vector field of
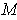 if each of the
if each of the
 are
differentiable vector fields of each
are
differentiable vector fields of each
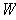 . In particular, if
. In particular, if
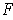 is the
restriction of a differentiable vector field on some open subset
is the
restriction of a differentiable vector field on some open subset
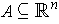 containing
containing
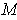 ,
then
,
then
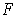 restricts to a differentiable vector field on
restricts to a differentiable vector field on
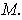
Similarly, a differentiable k-form on
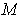 is a function
is a function
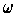 which assigns to each
which assigns to each
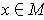 an
an
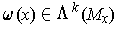 such that
such that
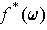 is a differentiable k-form on
is a differentiable k-form on
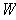 for every coordinate system
for every coordinate system
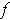 about
about
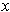 . The derivative
. The derivative
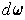 of
of
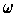 is the differentiable
k-form on
is the differentiable
k-form on
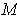 provided by the following result:
provided by the following result:
Proposition 2: If
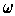 is a differentiable k-form on
is a differentiable k-form on
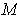 , then
there is a unique differentiable
, then
there is a unique differentiable
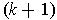 -form on
-form on
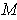 such that for every
coordinate system
such that for every
coordinate system
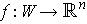 about
about
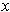 , one has
, one has
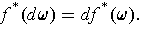
Proof: For each
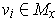 , let
, let
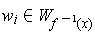 be chosen
so that
be chosen
so that
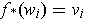 . Let
. Let
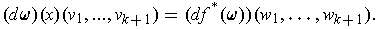
This definition is independent of the choice of coordinate system
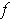 and
is easily shown to be the desired differentiable
and
is easily shown to be the desired differentiable
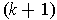 -form on
-form on
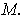
Let
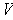 be a finite dimensional real vector space of dimension
be a finite dimensional real vector space of dimension
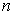 and
and
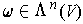 be non-zero. Then
be non-zero. Then
 is non-zero for every basis
is non-zero for every basis
 of
of
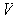 . Thus, the set of
(ordered) bases of
. Thus, the set of
(ordered) bases of
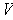 is partitioned into two sets, such that two bases are in
the same set if and only if
is partitioned into two sets, such that two bases are in
the same set if and only if
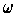 applied to the bases gives a real
number of the same sign. The set to which an (ordered) basis belongs is
called its orientation and is denoted
applied to the bases gives a real
number of the same sign. The set to which an (ordered) basis belongs is
called its orientation and is denoted
 Note that
two bases being of the same orientation is independent of the choice of
Note that
two bases being of the same orientation is independent of the choice of
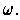 The usual orientation of
The usual orientation of
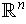 is defined to
be
is defined to
be

Suppose that for every
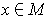 (where
(where
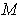 is a k-dimensional manifold),
one has chosen
is a k-dimensional manifold),
one has chosen
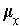 an orientation of the tangent space
an orientation of the tangent space
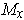 . Then these
choices are said to be consistent if and only if for every
coordinate system
. Then these
choices are said to be consistent if and only if for every
coordinate system
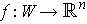 about
about
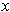 and every pair
and every pair
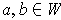 ,
one has
,
one has
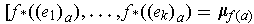 if and only if
if and only if
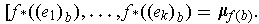 Such a consistent
choice is called an orientation of
Such a consistent
choice is called an orientation of
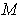 ; a manifold which admits
an orientation is said to be orientable.
; a manifold which admits
an orientation is said to be orientable.
If the
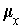 are consistent, then one says that the coordinate system
are consistent, then one says that the coordinate system
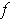 is said to be orientation preserving
if
is said to be orientation preserving
if
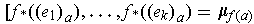 for every
for every
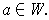 Clearly, if
Clearly, if
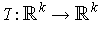 is a linear transformation
with
is a linear transformation
with
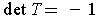 , then exactly one of
, then exactly one of
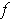 and
and
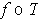 is orientation
preserving.
is orientation
preserving.
Now, let
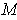 be a
be a
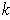 -dimensional manifold-with-boundary and
-dimensional manifold-with-boundary and
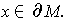 Then
Then
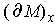 is a
is a
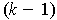 -dimensional subspace of
-dimensional subspace of
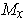 . There are
precisely two unit vectors perpendicular to this subspace. Choose a
coordinate system
. There are
precisely two unit vectors perpendicular to this subspace. Choose a
coordinate system
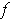 about
about
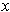 in which 0 maps to
in which 0 maps to
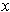 and
and
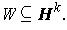 Then the one of the unit vectors of the form
Then the one of the unit vectors of the form
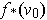 with
with
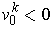 is
called the outward unit normal
is
called the outward unit normal
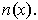 Suppose we have an
orientation
Suppose we have an
orientation
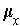 for
for
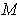 . Then choose
. Then choose
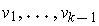 a basis
for
a basis
for
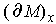 such that
such that
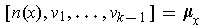 . Then
the
. Then
the
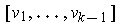 define a consistent orientation on
define a consistent orientation on
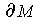 called the induced orientation. Note that the orientation induced
on
called the induced orientation. Note that the orientation induced
on
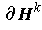 from the usual orientation on
from the usual orientation on
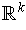 is the
usual orientation if and only if
is the
usual orientation if and only if
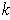 is even.
is even.
If
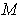 is
is
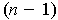 -dimensional manifold contained in
-dimensional manifold contained in
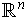 which
admits an orientation
which
admits an orientation
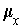 , then one can also define an outward unit normal
, then one can also define an outward unit normal
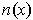 as the one such that if
as the one such that if
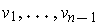 is a basis of
is a basis of
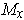 with
with
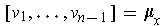 , then
, then
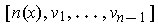 is the
usual orientation of
is the
usual orientation of
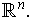
If
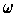 is a
is a
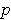 -form on a
-form on a
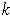 -dimensional manifold-with-boundary
-dimensional manifold-with-boundary
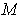 and
and
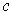 is a singular
is a singular
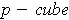 in
in
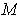 , we can define:
, we can define:
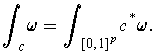
Integrals over
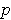 -chains are defined in the obvious way. In the special
case where
-chains are defined in the obvious way. In the special
case where
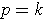 , we will always assume that
, we will always assume that
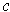 is the restriction
to
is the restriction
to
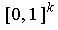 of a coordinate system
of a coordinate system
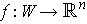 (where
we assume
(where
we assume
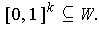 If one has an orientation for
If one has an orientation for
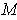 , we say
that the singular
, we say
that the singular
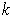 -cube is orientation preserving provided that
-cube is orientation preserving provided that
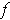 is.
is.
All the definitions have been set up to guarantee the following result:
Proposition 3: If
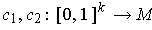 are two orientation
preserving singular
are two orientation
preserving singular
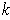 -cubes in an oriented
-cubes in an oriented
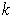 -dimensional manifold
-dimensional manifold
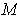 and
and
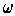 is a
is a
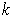 -form on
-form on
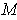 such that
such that
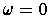 outside of
outside of
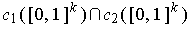 , then
, then
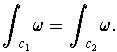
Proof: We have
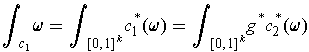
where
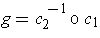 and we have used the assumption that
and we have used the assumption that
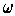 is zero outside of
is zero outside of
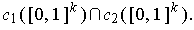 It remains to show that
It remains to show that
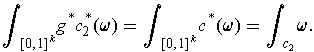
But, if
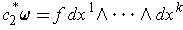 , then we have
, then we have
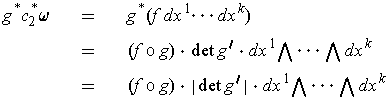
since
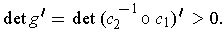 The result now follows by
the change of variables formula for integrals.
The result now follows by
the change of variables formula for integrals.
We can now define integrals. Let
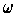 be a k-form on an oriented
k-dimensional manifold
be a k-form on an oriented
k-dimensional manifold
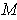 . Choose an open cover
. Choose an open cover
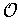 of
of
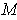 such that for each
such that for each
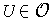 , there is an orientation preserving
singular
, there is an orientation preserving
singular
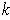 -cube
-cube
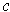 with
with
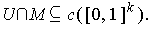 Let
Let
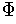 be
a partition of unity for
be
a partition of unity for
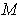 subordinate to this cover. Define
subordinate to this cover. Define
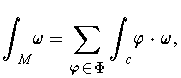
where
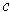 was chosen so that
was chosen so that
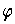 is zero outside of an compact subset
of
is zero outside of an compact subset
of
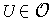 and
and
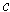 is is an orientation preserving singular
is is an orientation preserving singular
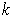 -cube
with
-cube
with
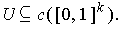 Then just as in Chapter 3, the value of
this integral is independent of the choice of
Then just as in Chapter 3, the value of
this integral is independent of the choice of
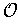 ,
,
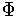 , and
, and
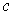 .
.
Now suppose we have a
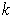 -dimensional manifold-with-boundary
-dimensional manifold-with-boundary
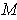 with
orientation
with
orientation
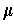 . Let
. Let
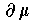 be the orientation induced by
be the orientation induced by
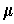 on
on
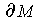 . Let
. Let
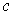 be an orientation-preserving
be an orientation-preserving
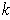 -cube in
-cube in
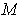 such that
such that
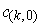 lies in
lies in
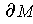 and this is the only face which
contains any interior points of
and this is the only face which
contains any interior points of
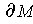 . Then
. Then
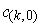 is orientation
preserving if and only
is orientation
preserving if and only
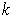 is even. In particular, if
is even. In particular, if
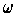 is
a
is
a
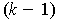 -form on
-form on
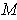 which is zero outside of
which is zero outside of
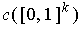 , we have
, we have
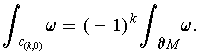
Now
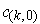 appears with coefficient
appears with coefficient
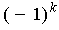 in the definition of
in the definition of
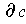 . So,
. So,
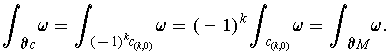
This explains the strange choice of signs in the definition of the induced
orientation on
Theorem 1: (Stokes' Theorem) Let
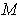 be a compact oriented
be a compact oriented
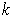 -dimensional
manifold-with-boundary and
-dimensional
manifold-with-boundary and
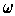 be a
be a
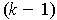 -form on
-form on
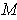 . Then
. Then
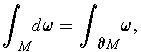
where
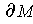 is oriented with the orientation induced from that of
is oriented with the orientation induced from that of
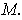
Proof: Begin with two special cases: First assume that there is
an orientation preserving
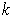 -cube in
-cube in
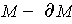 such that
such that
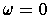 outside of
outside of
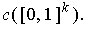 Using our earlier Stokes' Theorem, we get
Using our earlier Stokes' Theorem, we get
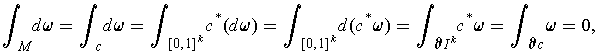
since
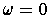 on
on
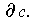 But
But
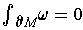 also
since
also
since
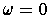 on
on
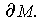
The second case is where there is an orientation-preserving singular
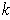 -cube in
-cube in
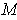 such that
such that
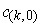 is the only face containing points
of
is the only face containing points
of
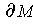 and
and
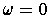 outside of
outside of
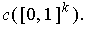 One has:
One has:
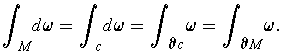
For the general case, choose an open cover
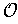 of
of
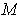 and a
partition of unity
and a
partition of unity
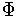 subordinate to
subordinate to
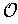 such that for each
such that for each
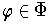 , the form
, the form
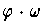 is as in one of the two cases
already considered. Since
is as in one of the two cases
already considered. Since
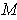 is compact, one has a finite sum:
is compact, one has a finite sum:
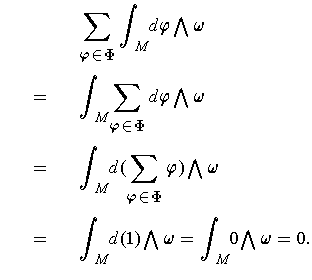
But then,
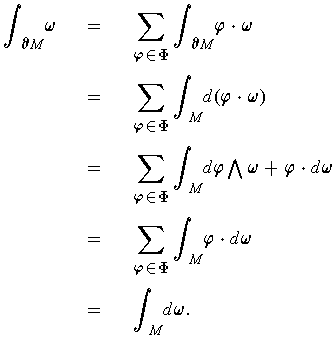
In
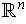 , the volume can be calculated as the integral
of the form
, the volume can be calculated as the integral
of the form
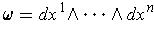 . We would like to find
a generalization to manifolds of this differential form.
. We would like to find
a generalization to manifolds of this differential form.
If
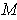 is a
is a
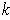 -dimensional manifold, then the usual inner product
on
-dimensional manifold, then the usual inner product
on
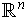 induces an inner product on each of the tangent spaces of
induces an inner product on each of the tangent spaces of
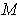 . (Recall that an inner product of V is a bilinear form
. (Recall that an inner product of V is a bilinear form
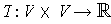 such that
such that
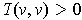 for all
for all
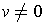 .) With an inner product, one
can define an orthonormal basis to be one of the form
.) With an inner product, one
can define an orthonormal basis to be one of the form
 where
where
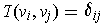 where
where
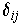 is the Kronecker
is the Kronecker
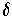 . Now, if
. Now, if
 and
and
 are both
orthonormal bases, then we can write
are both
orthonormal bases, then we can write
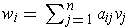 .
In particular, one calculates:
.
In particular, one calculates:
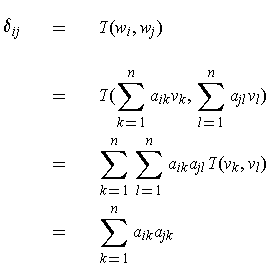
which can be expressed as a matrix equation
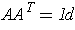 where
where
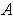 is the
matrix with entries
is the
matrix with entries
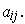 Taking determinants of this means that
Taking determinants of this means that
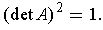 In particular, if
In particular, if
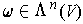 where
where
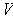 is a vector space of dimension
is a vector space of dimension
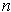 , then
, then
Proposition 4:
 is constant for all
orthonormal bases of
is constant for all
orthonormal bases of
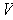 of the same orientation.
of the same orientation.
Definition 3: Let
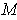 be an oriented
be an oriented
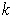 -dimensional manifold in
-dimensional manifold in
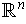 .
Then a
.
Then a
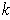 -form
-form
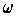 on
on
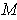 is called a volume element if
is called a volume element if
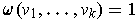 for all orientation preserving
orthonormal bases
for all orientation preserving
orthonormal bases

Example: Consider the case of 2-dimensional oriented manifolds
in
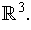 Let
Let
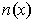 be the outward normal at
be the outward normal at
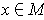 . Then
define
. Then
define
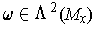 by
by
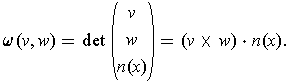
By the definition of the outward normal,
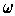 is a volume element.
Further, if
is a volume element.
Further, if
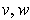 is an orthonormal basis of the same orientation as
is an orthonormal basis of the same orientation as
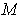 ,
one has:
,
one has:
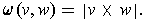
Also, expanding as cofactors of the last row, one gets
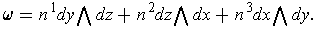
On
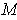 , one can compute for
, one can compute for
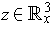 using
using
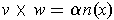 for some
for some
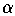 , that
, that
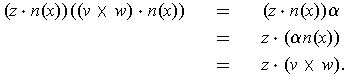
Letting
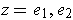 , and
, and
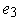 , we get:
, we get:
Proposition 4: Let
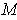 be an oriented 2-dimensional manifold in
be an oriented 2-dimensional manifold in
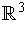 and let
and let
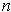 be the unit outward normal. Then
the volume element
be the unit outward normal. Then
the volume element
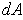 satisfies:
satisfies:
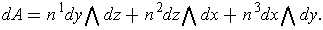
Further, on
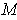 , one has:
, one has:
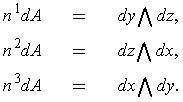
To calculate a surface area, we need to evaluate
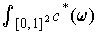 for an orientation preserving singular 2-cube
for an orientation preserving singular 2-cube
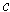 . The integrand is
. The integrand is
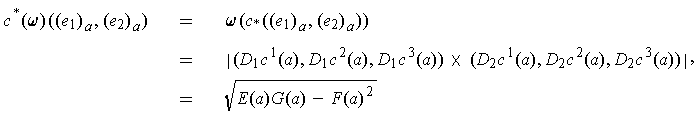
where
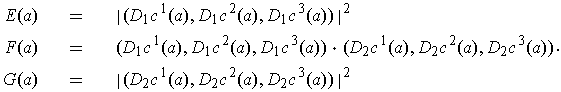
(See Problem 4.9, part e.)
Three separate results will be shown to be special cases of our Stokes' Theorem.
Theorem 2: (Green's Theorem) Let
 be a
compact 2-dimensional manifold-with-boundary. Suppose that
be a
compact 2-dimensional manifold-with-boundary. Suppose that
 are differentiable. Then
are differentiable. Then
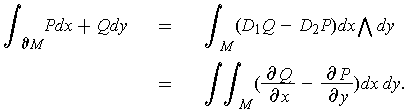
Proof: This is just Stoke's Theorem in the case of a 1-form.
Theorem 3: (Divergence Theorem) Let
 be
a compact 3-dimensional manifold-with-boundary and
be
a compact 3-dimensional manifold-with-boundary and
 be the unit outward
normal on
be the unit outward
normal on
 . Let
. Let
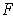 be a differentiable vector field on
be a differentiable vector field on
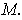 Then
Then
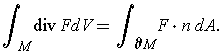
In terms of
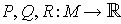 , this amounts to:
, this amounts to:
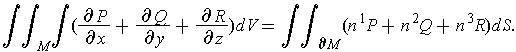
Proof: Define
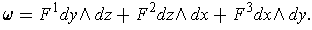 Then
Then
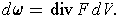 Further, Proposition 4 says that:
Further, Proposition 4 says that:
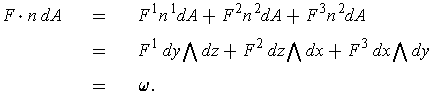
So, we see that this is also a special case of Stokes' Theorem
Theorem 4: (Stokes' Theorem) Let
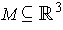 be a
compact oriented 2-dimensional manifold-with-boundary and
be a
compact oriented 2-dimensional manifold-with-boundary and
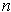 be the unit
outward normal on
be the unit
outward normal on
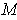 determined by the orientation on
determined by the orientation on
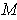 . Let
. Let
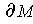 have the induced orientation. Let
have the induced orientation. Let
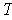 be the vector field on
be the vector field on
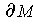 with
with
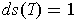 and
and
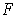 be a differentiable vector field in an open set
containing
be a differentiable vector field in an open set
containing
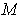 . Then
. Then
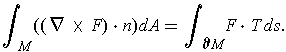
In terms of
 , this amounts to:
, this amounts to:
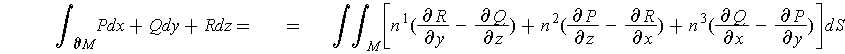
Proof: Let
 on
on
 be defined by
be defined by
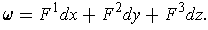 Again, using Proposition 4, we get:
Again, using Proposition 4, we get:
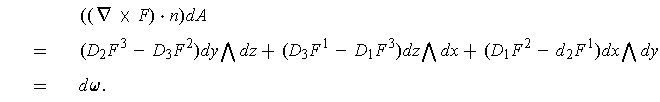
Since
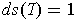 , one has
, one has
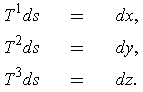
as one can see by evaluating each equation at
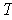 .
It follows that
.
It follows that
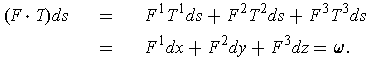
So, this is also a special case of our earlier Stokes' Theorem.